本文并非原创，而是参考以下文章写就，涉及到论文的部分则是去原始论文中来替换，确保原汁原味且没有错误。如有错误，还望批评指正。

【参考文章】：

Bandit 算法与推荐系统 | 统计之都

Bandit算法，A/B测试，孰优孰劣？ - 云+社区 - 腾讯云

科学网-Bandit:一种简单而强大的在线学习算法 - 范深的博文

推荐系统遇上深度学习(十二)--推荐系统中的EE问题及基本Bandit算法 - 简书

【总结】Bandit算法与推荐系统 - 一寒惊鸿 - CSDN博客

[1] - Bandit算法的起源

Bandit算法来源于历史悠久的赌博学，它要解决的问题是这样的^[1]：一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么每次该选择哪个老虎机可以做到最大化收益呢？这就是多臂赌博机问题 ( Multi-armed bandit problem, K-armed bandit problem, MAB )。

解决这个问题最好的办法是去试，但不是盲目地试，而是有策略地快速试一试，这些策略就是Bandit算法。

假设我们已经经过一些试验，得到了当前每个老虎机的吐钱的概率，如果想要获得最大的收益，我们会一直摇那个吐钱概率最高的老虎机，这就是 Exploitation 。但是，当前获得的信息并不是老虎机吐钱的真实概率，可能还有更好的老虎机吐钱概率更高，因此还需要进一步探索，这就是 Exploration 问题。

这个多臂问题，推荐系统里很多问题都与它类似：

1. 假设一个用户对不同类别的内容感兴趣程度不同，那么我们的推荐系统初次见到这个用户时，怎么快速地知道他对每类内容的感兴趣程度？这就是推荐系统的冷启动。
2. 假设我们有若干广告库存，怎么知道该给每个用户展示哪个广告，从而获得最大的点击收益？是每次都挑效果最好那个么？那么新广告如何才有出头之日？
3. 我们的算法工程师又想出了新的模型，有没有比A/B test更快的方法知道它和旧模型相比谁更靠谱？
4. 如果只是推荐已知的用户感兴趣的物品，如何才能科学地冒险给他推荐一些新鲜的物品？

[2] - Bandit 算法和推荐系统

Exploration and Exploitation(EE问题，探索与开发) 是计算广告和推荐系统里常见的一个问题。其中，Exploitation就是：对用户比较确定的兴趣，当然要利用开采迎合，好比说已经挣到的钱，当然要花；而Exploration就是：光对着用户已知的兴趣使用，用户很快会腻，所以要不断探索用户新的兴趣才行，这就好比虽然有一点钱可以花了，但是还得继续搬砖挣钱，不然花完了就得喝西北风。

用户冷启动问题，也就是面对新用户时，如何能够通过若干次实验，猜出用户的大致兴趣。

用 Bandit 算法解决冷启动的大致思路如下：用分类或者 Topic 来表示每个用户兴趣，也就是 MAB 问题中的臂 ( Arm ) ，我们可以通过几次试验，来刻画出新用户心目中对每个Topic的感兴趣概率。这里，如果用户对某个 Topic 感兴趣（提供了显式反馈或隐式反馈），就表示我们得到了收益，如果推给了它不感兴趣的 Topic ，推荐系统就表示很遗憾 ( regret ) 了。如此经历“选择-观察-更新-选择”的循环，理论上是越来越逼近用户真正感兴趣的 Topic 的。

[3] - 相关概念

通常使用累积遗憾^[2] (regret) 来衡量不同 Bandit 算法在解决多臂问题上的效果。

是第 次试验时被选中臂的期望收益， 是所有臂中最优的那个，如果上帝提前告诉我们，我们当然每次试验都选它，问题是上帝不告诉我们。这个公式可以用来对比不同 Bandit 算法的效果：对同样的多臂问题，用不同的 Bandit 算法试验相同次数，看看谁的 regret 增长得慢。

[4] - 经典 Bandit 算法

朴素 Bandit 算法

先随机试若干次，计算每个臂的平均收益，一直选均值最大那个臂。这个算法是人类在实际中最常采用的，不可否认，它还是比随机乱猜要好。

Epsilon-Greedy 算法

这个算法有点类似模拟退火的思想。选一个 之间较小的数 ，每次以 的概率在所有臂中随机选一个。以 的概率选择截止当前，平均收益最大的那个臂。根据选择臂的回报值来对回报期望进行更新。

这里 的值可以控制对 exploit 和 explore 的偏好程度，每次决策以概率 去 Exploration ， 的概率来 Exploitation 。

Thompson sampling 算法

Thompson sampling^[3] 算法用到了 ^[4]分布。假设每个臂是否产生收益，其背后有一个概率分布，产生收益的概率为 ，同时该概率 的概率分布符合 分布，每个臂都维护一个 分布的参数，即 。每次试验后，选中一个臂摇一下，有收益则该臂的 增加 ，否则该臂的 增加 。

每次选择臂的方式是：用每个臂现有的 分布产生一个随机数，选择所有臂产生的随机数中最大的那个臂去摇。

UCB 算法

UCB 算法全称是 Upper Confidence Bound（置信区间上界）。算法步骤^[5]：先对每一个臂都试一遍，之后在任意时刻 按照如下公式计算每个臂的分数，然后选择分数最大的臂作为选择

观察选择结果，更新 和 。其中 表示的是the average reward obtained from machine j， ，后面的叫做bonus，本质上是均值的标准差， 是目前的试验次数， 是the number of times j has been played so far。

显然，以上四种算法中，UCB算法和Thompson采样算法更优秀一些 。这里^[6]有以上四种代码的实现方式以及一个简单的效果评估实验。

[5] - LinUCB — 改造后的 UCB 算法

UCB 算法在做 EE ( Exploit-Explore ) 的时候表现不错，但它是上下文无关 (context free) 的 bandit 算法，它只管埋头干活，根本不观察一下面对的都是些什么特点的 arm，下次遇到相似特点但不一样的 arm 也帮不上什么忙。

UCB 解决 Multi-armed bandit 问题的思路是：用置信区间。置信区间可以简单地理解为不确定性的程度，区间越宽，越不确定。每个 item 的回报均值都有个置信区间，随着试验次数增加，置信区间会变窄（逐渐确定了到底回报丰厚还是可怜）。每次选择前，都根据已经试验的结果重新估计每个 item 的均值及置信区间，选择置信区间上限最大的那个 item。这句话反映了几个意思：

1. 如果 item 置信区间很宽（被选次数很少，还不确定），那么它会倾向于被多次选择，这个是算法冒风险的部分；
2. 如果 item 置信区间很窄（备选次数很多，比较确定其好坏了），那么均值大的倾向于被多次选择，这个是算法保守稳妥的部分；
3. UCB 是一种乐观的算法，选择置信区间上界排序，如果是悲观保守的做法，是选择置信区间下界排序。

Yahoo! 的科学家们在 2010 年发表了一篇论文^[7]，给 UCB 引入了特征信息，同时还把改造后的 UCB 算法用在了 Yahoo! 的新闻推荐中，算法名叫 LinUCB ，刘鹏博士在《计算广告》^[8]一书中也有介绍 LinUCB 在计算广告中的应用。

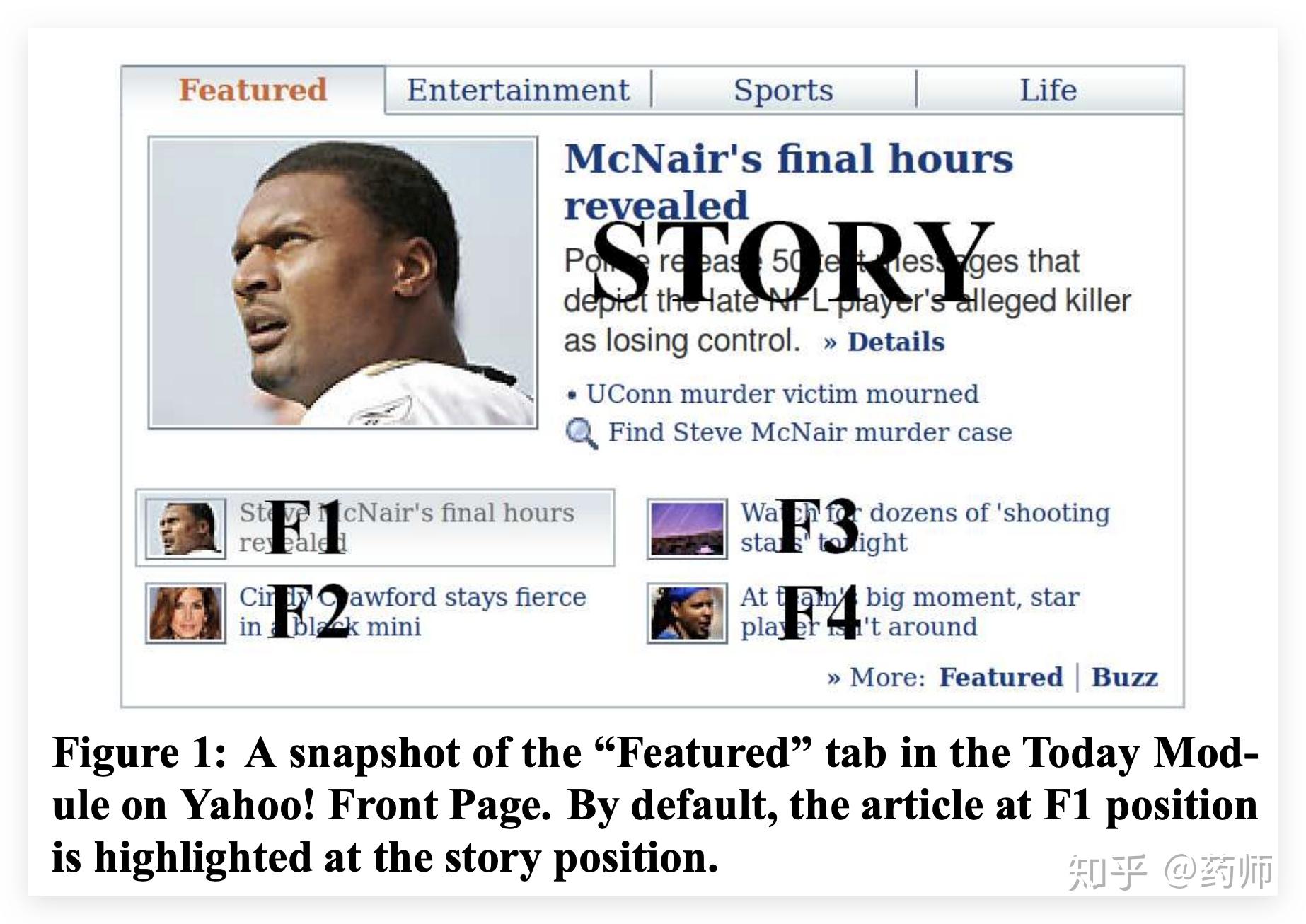
单纯的老虎机回报情况就是老虎机自己内部决定的，而在广告推荐领域，一个选择的回报，是由 User 和 Item 一起决定的，如果我们能用 feature 来刻画 User 和 Item 这一对 CP，在每次选择 item 之前，通过 feature 预估每一个 arm (item) 的期望回报及置信区间，选择的收益就可以通过 feature 泛化到不同的 item 上。为 UCB 算法插上了特征的翅膀，这就是 LinUCB 最大的特色。

LinUCB 算法做了一个假设：一个 Item 被选择后推送给一个 User，其回报和相关 Feature 成线性关系，这里的 “相关 feature” 就是 context，也是实际项目中发挥空间最大的部分。于是试验过程就变成：用 User 和 Item 的特征预估回报及其置信区间，选择置信区间上界最大的 item 推荐，观察回报后更新线性关系的参数，以此达到试验学习的目的。

上图是论文中给出的 LinUCB 算法，其中参数 决定了 Explore 的程度。如第二行所示，首先获取每一个 arm 的特征向量 。接下来开始计算每一个 arm 的预估回报及其置信区间，如果 arm 还未被试验过，那么用单位矩阵初始化 ，用 向量初始化 。接着，计算线性参数 ，用 和特征向量 计算预估回报，同时加上置信区间宽度。处理完每一个 arm 之后，选择计算出的最大值对应的 arm ，观察真实的回报 ，最后更新 和 。

注意到上面算法中给特征矩阵加了一个单位矩阵，这就是岭回归^[9] (ridge regression)，岭回归主要用于当样本数小于特征数时，对回归参数进行修正。 对于加了特征的 bandit 问题，正符合这个特点：试验次数（样本）少于特征数。每一次观察真实回报之后，要更新的不止是岭回归参数，还有每个 arm 的回报向量 。

LinUCB 算法有一个很重要的步骤，就是给 User 和 Item 构建特征，也就是刻画 context。在原始论文里，Item 是文章，其中专门介绍了它们是怎么构建特征的。

【原始用户特征】有：人口统计学，性别特征（2 类），年龄特征（离散成 10 个区间）；地域信息，遍布全球的大都市，美国各个州；行为类别，代表用户历史行为的 1000 个类别取值。

【原始文章特征】：URL 类别，根据文章来源分成了几十个类别；编辑打标签，编辑人工给内容从几十个话题标签中挑选出来的。

原始特征向量都要归一化成单位向量。还要对原始特征降维，以及模型要能刻画一些非线性的关系。 用 Logistic Regression 去拟合用户 对文章 的点击历史，其中的线性回归部分为：

拟合得到参数矩阵 ，其中 和 分别对应特征向量。之后，可以将原始用户特征（1000 多维）投射到文章的原始特征空间（80 多维），投射计算方式：

然后，用投射后的 80 多维特征对用户聚类（可以使用 K-means），得到 5 个类簇，文章页同样聚类成 5 个簇，再加上常数 1，用户和文章各自被表示成 6 维向量。Yahoo! 的科学家们之所以选定为 6 维，因为数据表明它的效果最好^[10]，并且这大大降低了计算复杂度和存储空间。

LinUCB 算法有以下优点：由于加入了特征，所以收敛比 UCB 更快（论文有证明）；特征构建是效果的关键，也是工程上最麻烦和值的发挥的地方；由于参与计算的是特征，所以可以处理动态的推荐候选池，编辑可以增删文章；特征降维很有必要，关系到计算效率。

[6] - Bandit 算法与协同过滤

推荐系统里面，传统经典的算法肯定离不开协同过滤，协同过滤背后的思想简单深刻。协同过滤看上去是一种算法，不如说是一种方法论，不是机器在给你推荐，而是 “集体智慧” 在给你推荐。

它的基本假设就是 “物以类聚，人以群分”，你的圈子决定了你能见到的物品。这个假设很靠谱，却隐藏了一些重要的问题：作为用户的我们还可能看到新的东西吗？还可能有惊喜吗？还可能有圈子之间的更迭流动吗？这些问题的背后其实就是在前面提到过的 EE 问题（Exploit & Explore）。我们关注推荐的准确率，但是我们也应该关注推荐系统的演进发展，因为 “推荐系统不止眼前的 Exploit，还有远方的 Explore”。

做 Explore 的方法有很多，bandit 算法是其中的一种流派，前面也进行了许多介绍。那 bandit 算法，能不能和协同过滤这种算法结合起来呢？事实上已经有人做过了，叫做 COFIBA 算法，具体在题目为 《Collaborative Filtering Bandits》^[11] 和《Online Clustering of Bandits》^[12] 的两篇文章中有详细的描述，两篇文章的区别是后者只对用户聚类（即只考虑了 User-based 的协同过滤），而前者采用了协同聚类（co-clustering，可以理解为 item-based 和 user-based 两种协同方式在同时进行），后者是前者的一个特殊情况。

很多推荐场景中都有这两个规律：相似的用户对同一个物品的反馈可能是一样的。也就是对一个聚类用户群体推荐同一个 item，他们可能都喜欢，也可能都不喜欢，同样地，同一个用户会对相似的物品反馈相同，这是属于协同过滤可以解决的问题；在使用推荐系统过程中，用户的决策是动态进行的，尤其是新用户。这就导致无法提前为用户准备好推荐候选，只能 “走一步看一步”，是一个动态的推荐过程。

每一个推荐候选 item，都可以根据用户对其偏好不同（payoff 不同）将用户聚类成不同的群体，一个群体来集体预测这个 item 的可能的收益，这就有了协同的效果，然后再实时观察真实反馈回来更新用户的个人参数，这就有了 bandit 的思想在里面。

另外，如果要推荐的候选 item 较多，还需要对 item 进行聚类，这样就不用按照每一个 item 对 user 聚类，而是按照每一个 item 的类簇对 user 聚类，如此以来，item 的类簇数相对于 item 数要大大减少。

基于这些思想，有人提出了算法 COFIBA^[13]（读作 coffee bar）

在时刻 t，用户来访问推荐系统，推荐系统需要从已有的候选池子中挑一个最佳的物品推荐给他，然后观察他的反馈，用观察到的反馈来更新挑选策略。 这里的每个物品都有一个特征向量，所以这里的 bandit 算法是 context 相关的。 这里依然是用岭回归去拟合用户的权重向量，用于预测用户对每个物品的可能反馈 (payoff)，这一点和 linUCB 算法是一样的。

对比 LinUCB 算法，COFIBA 算法的不同有两个：基于用户聚类挑选最佳的 item（相似用户集体决策的 bandit）；基于用户的反馈情况调整 user 和 item 的聚类（协同过滤部分）。

算法针对某个用户 ，首先计算该用户的 bandit 参数 （和 LinUCB 相同），但是这个参数并不直接参与到 bandit 的选择决策中（和 LinUCB 不同），而是用来更新用户聚类的；接着遍历候选 item，每一个 item 表示成一个 context 向量；这样，每一个 item 都对应一套用户聚类结果，所以遍历到每一个 item 时判断当前用户在当前 item 下属于哪个类簇，然后把对应类簇中每个用户的 矩阵 (对应 LinUCB 里面的 A 矩阵)， 向量（payoff 向量，对应 LinUCB 里面的 向量）聚合起来，从而针对这个类簇求解一个岭回归参数（类似 LinUCB 里面单独针对每个用户所做），同时计算其 payoff 预测值和置信上边界；然后，每个 item 都得到一个 payoff 预测值及置信区间上界，挑出那个上边界最大的 item 推出去（和 LinUCB 相同）；观察用户的真实反馈，然后更新用户自己的 矩阵和 向量（更新个人的，对应类簇里其他的不更新）。

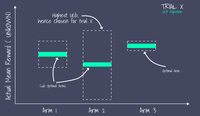
以上是 COFIBA 算法的一次决策过程。在收到用户真实反馈之后，还有两个计算过程：更新 user 聚类和更新 item 聚类。论文中给出的更新 user 和 item 的聚类示意图如下所示。

解释一下这个图。

（a）这里有 个 user、 个 item，初始化时，user 和 item 的类簇个数都是
（b1）在某一轮试验时，推荐系统面对的用户是 。推荐过程就是遍历 1～8 每个 item，然后看看对应每个 item 时，user 在哪个类簇中，把对应类簇中的用户聚合起来为这个 item 预测 payoff 和 CB。这里假设最终 item 胜出，被推荐出去了。
（b2）在时刻 ，item 有 个类簇，需要更新的用户聚类是 item 对应的 user 所在类簇。更新方式：看看该类簇里面除了 user 之外的用户，对 item 的 payoff 是不是和 user 相近，如果是，则保持原来的连接边，否则删除原来的连接边。删除边之后重新构建聚类结果。这里假设重新构建后原来 user 所在的类簇分裂成了两个类簇：{4,5} 和 {6}
（c）更新完用户类簇后，item 对应的类簇也要更新。方式是：对于每一个和 item （被推荐出的那个 item）还存在连接边的 item ，都去构造一个 user 的近邻集合 ，这个集合的用户对 item 有相近的 payoff，然后看 是不是和刚刚更新后的 user 4 所在的类簇相同，是的话，保留 item 和 item 之间的连接边，否则删除。这里假设 item 和 item 之间的连接边被删除。item 独立后给它初始化了一个聚类结果：所有用户还是一个类簇。

简单来说就是：

• User-based 协同过滤来选择要推荐的 item，选择时用了 LinUCB 的思想
• 根据用户的反馈，调整 User-based 和 Item-based 的聚类结果
• Item-based 的聚类变化又改变了 User 的聚类
• 不断根据用户实时动态的反馈来划分 User-Item 矩阵

有兴趣可以直接去看原始论文。

[7] - 总结

Exploit-Explore 这一对矛盾一直客观存在，bandit 算法是公认的一种比较好的解决 EE 问题的方案。除了 bandit 算法之外，还有一些其他的 explore 的办法，比如：在推荐时，随机地去掉一些用户历史行为（特征）。解决 Explore，势必就是要冒险，势必要走向未知，而这显然就是会伤害用户体验的：明知道用户肯定喜欢 A，你还偏偏以某个小概率给推荐非 A。

实际上，很少有公司会采用这些理性的办法做 Explore，反而更愿意用一些盲目主观的方式。究其原因，可能是因为：

1. 互联网产品生命周期短，而 Explore 又是为了提升长期利益的，所以没有动力做；
2. 用户使用互联网产品时间越来越碎片化，Explore 的时间长，难以体现出 Explore 的价值；
3. 同质化互联网产品多，用户选择多，稍有不慎，用户用脚投票，分分钟弃你于不顾。
4. 已经成规模的平台，红利杠杠的，其实是没有动力做 Explore 的；

基于这些，我们如果想在自己的推荐系统中引入 Explore 机制，需要注意以下几点：

1. 用于 Explore 的 item 要保证其本身质量，纵使用户不感兴趣，也不至于引起其反感；
2. Explore 本身的产品需要精心设计，让用户有耐心陪你玩儿；
3. 深度思考，这样才不会做出脑残的产品，产品不会早早夭折，才有可能让 Explore 机制有用武之地

参考

1. ^https://en.wikipedia.org/wiki/Multi-armed_bandit
2. ^https://nbviewer.jupyter.org/github/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/blob/master/Chapter6_Priorities/Ch6_Priors_PyMC3.ipynb#A-Measure-of-Good
3. ^https://en.wikipedia.org/wiki/Thompson_sampling
4. ^https://zh.wikipedia.org/wiki/%CE%92%E5%88%86%E5%B8%83
5. ^http://hunch.net/~coms-4771/lecture20.pdf
6. ^https://gist.github.com/anonymous/211b599b7bef958e50af
7. ^https://arxiv.org/pdf/1003.0146.pdf
8. ^《计算广告：互联网商业变现的市场与技术》P253，刘鹏、王超著
9. ^https://en.wikipedia.org/wiki/Tikhonov_regularization
10. ^http://www.gatsby.ucl.ac.uk/~chuwei/paper/isp781-chu.pdf
11. ^https://arxiv.org/pdf/1502.03473.pdf
12. ^https://arxiv.org/pdf/1401.8257.pdf
13. ^https://github.com/qw2ky/CoLinUCB_Revised/blob/master/COFIBA.py