看懂蒙特卡洛积分(一) 概率分布变换与随机采样

塔下意识粉, 跳刀躲梅肯

TC130：游戏渲染进阶zhuanlan.zhihu.com

蒙特卡洛积分是图形学中常用的数学工具, 这里就来总结下蒙特卡洛积分的原理和使用方式. 很多教程中把概率分布和积分是混在一起讲的, 个人觉得分开讲比较合适. 这篇文章就先来讲下概率分布变换和随机采样的部分.

概率论基础

这里快速回顾下概率论的基础, 这里不会特别深入精确地描述. 需要的朋友可以参考概率论相关的教材.

设 $X$ 是随机变量, $x$ 是任意实数, 称函数 $F(x) = P\{ X\leq x\}(x \in \bm R)$ 为随机变量 $X$ 的分布函数/CDF, 或称 $X$ 服从 $F(x)$ , 记为 $X\sim F(x)$ .

分布函数满足:

单调不减;
右连续, 即 $\lim_{x \rightarrow x_0^+}F(x) = F(x_0+0)=F(x_0)$ ;
$F(-\infty)=\lim_{x \rightarrow -\infty}F(x) = 0, F(+\infty)=\lim_{x \rightarrow +\infty}F(x) = 1$ .

从分布函数求概率:

$P(X \leq a) = F(a)$
$P(X < a) = F(a - 0)$
$P(X = a) = F(a) - F(a - 0)$

(1) 离散型变量

随机变量 $X$ 只能取有限个可能的值, 称 $X$ 为离散型随机变量, 称 $P\{X = x_i\} = p_i, i = 1, 2, 3...$ 为 $X$ 的概率分布, 记为 $X\sim p_i$ .

可以用矩阵形式表示为: $X\sim \begin{pmatrix} x_1 & x_2 & ... \\ p_1 & p_2 &... \end{pmatrix}$ .

离散型随机变量的概率分布满足 $\sum_{i}^{}{p_i} = 1$ .

比如记掷骰子的点数为 $X$ , 得

$X\sim \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 & \end{pmatrix}.\\$

$X$ 的分布函数为

$F(x) = \begin{cases} 0, & x <1,\\ 1/6& {1 \leq x < 2},\\ 1/3,& {2 \leq x < 3},\\ 1/2,& {3 \leq x < 4},\\ 2/3,& {4 \leq x < 5},\\ 5/6,& {5 \leq x < 6},\\ 1,& { x \geq 6}.\\ \end{cases}\\$

(2) 连续型变量

如果随机变量 $X$ 的分布函数可以表示为:

$F (x) = \int_{-\infty}^{x} f(t)dt \space (x \in \bm R, f(t)\geq 0)\\$

称 $X$ 为连续型随机变量, 称 $f(x)$ 为 $X$ 的概率密度函数/概率密度/PDF, 记为 $X\sim f(x)$ .

概率密度函数满足 $\int_{-\infty}^{+\infty} f(x)dx = 1$ .

对任意实数 $c$ , 有 $P\{ X = c\} = 0$ .

$X$ 取在某个区间的概率为:

$P\{ a < X < b\} =P\{ a \leq X < b\} = P\{ a < X \leq b\} \\=P\{ a \leq X \leq b\} =\int_{a}^{b} f(x)dx = F(b) - F(a)$

比如现在假设 $X$ 是一个均匀随机分布在 $(0, 2)$ 上的连续随机变量, 得

$f(x) = \begin{cases} 0, & x <0,\\ 1/2,& {0 \leq x < 2},\\ 0 ,& {x > 2}.\\ \end{cases}\\ F(x) = \begin{cases} 0, & x <0,\\ x/2,& {0 \leq x < 2},\\ 1 ,& {x > 2}.\\ \end{cases}\\$

(3) 如果 $X_1, X_2, ...X_n$ 是定义在样本空间上n个随机变量, 则称 $(X_1, X_2, ...X_n)$ 为n维随机变量.

n维随机变量的分布函数定义为

$F(X_1, X_2, ...X_n) = P(X_1 \leq x_1, X_2 \leq x_2...X_n \leq x_n)\\$

n维随机变量的性质和上面类似, 这里不再一一描述.

随机值采样

在计算机中, 得到一个均匀随机分布在 $(0, 1)$ 上的随机数是很简单的, 我们这里用 $\xi$ 表示服从 $(0, 1)$ 均匀分布的随机变量. 现在我们就来用 $\xi$ 来得到我们想要的服从特定概率分布的随机变量.

(1) 离散型随机变量

对于离散型随机变量, 计算过程比较简单, 已知 $X\sim \begin{pmatrix} x_1 & x_2 & ... & x_n \\ p_1 & p_2 &... & p_n \end{pmatrix}$ , 假设从 $\xi$ 推导出 $X$ 的函数为 $X = G(\xi)$ .

考虑到 $\xi$ 在 $(0, 1)$ 上均匀分布, 只需要将 $\xi$ 依概率映射到 $X$ 样本空间中每个值即可. 得到

$X = G(\xi) = \begin{cases} x_1, & 0 < \xi <p_1,\\ x_2,& {p_1 \leq \xi < p_1 + p_2},\\ ...,& ...,\\ x_{n-1},& {\sum_{1}^{n-2}{p_i} \leq \xi < \sum_{1}^{n-1}{p_i}},\\ x_n,& { \sum_{1}^{n-1}{p_i} \leq \xi < 1}.\\ \end{cases}\\$

比如现在要得到

$X\sim \begin{pmatrix} 0 & 1 & 3 \\ 1/2 & 1/3 & 1/6 \end{pmatrix},\\$

易得

$X = G(\xi) = \begin{cases} 0, & 0 < \xi <1/2,\\ 1, & 1/2 \leq \xi <5/6,\\ 3, & 5/6\leq \xi < 1.\\ \end{cases}\\$

(2) 连续型随机变量

比如现在要得到概率密度为 $f(x)$ , 概率分布为 $F(x)$ 的随机变量 $X$ . 设变换函数为 $G$ , 即 $X=G(\xi)$ . 为了下面计算方便, 我们先假设 $F(x)$ 是一个单调递增函数.

由概率分布定义可知:

$P \{ X < a\} = F(a) \\ P \{ G(\xi) < a\} = F(a) \\$

已知 $G(\xi)$ 是单调递增函数, 可得:

$P \{\xi < G^{-1}(a) \} = F(a) \\$

已知 $\xi$ 在 $(0, 1)$ 上均匀分布, 可得

$P \{ \xi < b\} = b , b \in (0, 1) \\ P \{\xi < G^{-1}(a) \} = F(a) = G^{-1}(a)\\$

可以得到 $F, G$ 互为反函数, 即

$X = G(\xi) = F^{-1}(\xi)\\$

我们平时遇到的概率分布函数都是不满足单调递增的, 只需要去掉概率密度为0的部分即可.

现在举两个例子:

A. 次方分布

设 $X$ 在 $(0, 1)$ 上服从n次方分布, 即概率密度满足 $f(x) \propto x^n, x \in (0, 1)$ , 设 $f(x) = cx^n$ , 由概率密度性质可知

$\int_{-\infty}^{+\infty} f(x) = \int_{0}^{1} f(x) = \int_{0}^{1} cx^n = 1\\$

可以解得: $c = n + 1\\ f(x) = \begin{cases} (n + 1) x ^n, & x \in (0,1)\\ 0, & x \notin (0, 1) \end{cases}$

由此算出 $X$ 的概率分布函数:

$F(x) = \int_{-\infty}^{x} f(t) dt = \begin{cases} 0, & x \leq 0, \\ x^{n + 1}, & x\in (0, 1), \\ 1, & x \geq 1. \\ \end{cases}\\$

将 $F(x)$ 限制在 $(0, 1)$ 上, 可得

$X = G(\xi) = F^{-1}(\xi) = \sqrt[n + 1]{\xi}\\$

B. 指数分布

设 $X$ 的概率密度满足 $f(x) \propto e^{-ax}, x \in (0, +\infty)$ .

推导的部分和上面相同, 可得:

$f(x) = \begin{cases} 0, & x \leq 0,\\ ae^{-ax}, & x > 0;\\ \end{cases}\\ F(x) = \begin{cases} 0, & x \leq 0,\\ 1 - e^{-ax}, & x > 0;\\ \end{cases}\\ X = F^{-1}(\xi) = -\frac{ln(1-\xi)}{a}$

这里的 $1 - \xi$ 的概率分布和 $\xi$ 是相同的, 因此也可以写成

$X = -\frac{ln\xi}{a}\\$

(3) 拒绝式随机

对于一些无法求出解析解的概率分布函数, 或者无法得到 $f(x)$ 反函数的概率分布函数, 可以用拒绝式随机方法.

假设我们现在想得到一个概率密度为 $f(x)$ 的随机变量 $X$ .

现在我们已有一个概率密度为 $p(x)$ 的随机变量 , 我们可以任意次得到一个服从 $p(x)$ 分布的随机变量 $Y$ , 且其概率密度满足 $f(x) < cp(x), c \in R^+$ .

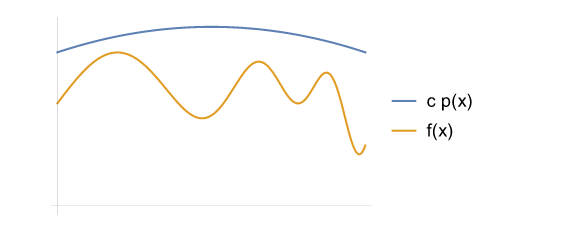
这样, 我们就可以通过下面的方法来随机得到 $X$ :

取一个服从 $p(x)$ 分布的随机变量值 $Y$ ;
在 $(0, 1)$ 上随机得到一个变量值 $\xi$ ;
如果 $cp(Y)\xi < f(Y)$ , 则该次随机结果被接受, 返回 $Y$ . 否者该次随机被拒绝, 重新执行第一步.

拒绝式随机方法的效率取决于 $cp(x)$ 和 $f(x)$ 之间的贴合程度, 如果二者之间空隙很大, 就可能需要多次随机, 效率会比较低.

一个常见的拒绝式随机法的应用场景就是随机在一个圆中取一个点, 大致过程为:

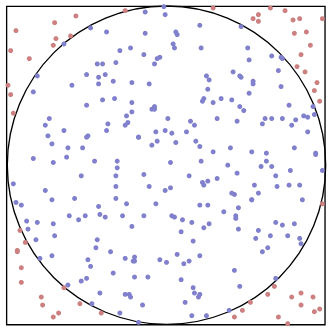
point p;
do {
  p.x = rand() * 2 - 1;
  p.y = rand() * 2 - 1;
} while(p.x * p.x + p.y + p.y > 1);
return p;

概率分布变换

现在已知一个随机变量 $X$ 的概率密度为 $f_X(x)$ , 现在我们令 $Y = T(X)$ , 现在我们要尝试求出 $Y$ 的概率密度函数 $f_Y(y)$ . 为了计算方便, 我们只考虑函数 $T$ 是严格单调递增的情况, 平时我们需要求解的函数大部分都是满足严格单调递增的.

由概率分布函数定义可知:

$P\{Y < T(x)\} = P\{ X < x \}\\ F_Y(y) =F_Y(T(x))= F_X(x)\\$

对两边一起求导得:

$f_Y(y) \frac{dy}{dx}= f_X(x)\\ f_Y(y) = ( \frac{dy}{dx})^{-1} f_X(x)\\$

这样, 我们成功计算出了 $Y$ 的概率密度函数.

比如现在有 $f_X = 2x, x\in(0, 1)$ , 令 $Y = \sin X$ , 可算出 $Y$ 的概率密度为:

$f_Y(y) = (\frac{dy}{dx})^{-1} f_X(x) = \frac{2x}{\cos x} = \frac{2\arcsin y}{\sqrt{1-y^2}}\\$

现在, 让我们来考虑多维随机变量, 设 $X$ 和 $Y$ 都是n维的随机变量, $X$ 和 $Y$ 之间的转换关系为 $Y = M(X)$ . $M$ 为矩阵函数, 即 $Y_i = M_i(X_1, X_2 ...X_n)$ , $M = (M_1, M_2 ...M_n)$ .

可以推导得出:

$f_Y(y) = f_Y(M(x)) = \frac{f_X(x)}{|J_T(x)|}\\$

${|J_T(x)|}$ 表示 $M$ 的雅可比矩阵的行列式的绝对值, $M$ 的雅可比矩阵为:

$\begin{pmatrix} \partial M_1/\partial x_1 & \cdots & \partial M_1/\partial x_n\\ \vdots & \ddots & \vdots \\ \partial M_n/\partial x_1 & \cdots & \partial M_n/\partial x_n\\ \end{pmatrix}\\$

现在来看下实际应用的例子:

A. 极坐标系

极坐标系的变换为

$x = r \cos \theta\\ y = r \sin \theta$

假设我们现在已知关于极坐标的概率密度函数 $f(r, \theta)$ , 现在来计算直角坐标系的概率密度.

对应的雅可比矩阵为:

$\begin{pmatrix} \partial x/\partial r & \partial x/\partial \theta\\ \partial y/\partial r & \partial y/\partial \theta\\ \end{pmatrix}\\$

求得行列式值为 $r(\cos^2 \theta + \sin ^2 \theta) = r$ . 这样, 我们得到两种坐标系之间的变换公式为:

$f(x, y) = \frac{f(r, \theta)}{r},\\ f(r, \theta) = r{f(x, y)}.\\$

B. 球坐标系

球坐标系到直角坐标系变换为:

$x = r \sin \theta \cos \phi\\ y = r \sin \theta \sin \phi\\ z = r \cos \theta$

可解得雅可比矩阵行列式值为 $|J_M| = r ^2 \sin\theta$ , 相应的概率密度为:

$f(r, \theta, \phi) = r^2 \sin\theta{f(x, y,z)}.\\$

现在来考虑在单位球面上的情况. 在球坐标系中, 我们从立体角的定义可以得到:

$d\omega = \sin\theta d\theta d \phi,\\$

立体角在某个 $\Omega$ 范围内的概率为:

$P\{ \omega \in \Omega \} = \int_{\Omega}^{} f(\omega) d\omega,\\$

得到概率密度的转换为:

$f(\theta, \phi) d\theta d\phi= f(\omega) d\omega,\\ f(\theta, \phi) = \sin \theta f(\omega).$

二维随机变量采样

现在可以来尝试从二维随机变量中采样.

(1) 联合概率密度

在开始之前, 我们还需要来简单回顾下联合概率密度的概念.

设现在有二维连续型随机变量 $(X, Y)$ , 二维随机变量的联合概率密度为 $f(x, y)$ , $(X, Y)$ 的联合分布函数为

$F(x, y) = \int_{-\infty}^{x} \int_{-\infty}^{y } f(u, v)du dv\\$

二维随机变量的概率密度满足

$f(x, y) \geq 0, \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty } f(x, y)dx dy = 1\\$

$X$ 的边缘概率密度为:

$f_X(x) = \int_{-\infty}^{+\infty} f(x, y) dy\\$

在 $X = x$ 的条件下, $Y$ 的条件概率密度为:

$f _{Y|X} (y | x) = \frac{f(x, y)}{f_X(x)}\\$

(2) 单位半球面采样

在单位半球面上均匀采样时, 每个立体角上都是等可能的. 由此得关于立体角的概率密度 $f(\omega)$ 是常数, 令其为 $c$ , 得

$\int_{H^2}^{} f(\omega) = \int_{H^2}^{} c = 1\\$

解得 $f(\omega) = c = \frac{1}{2 \pi}$ , 由前面得到的结论可知 $f(\theta, \phi) = \frac{\sin \theta}{2\pi}$ .

先来计算 $\theta$ , 得到 $\theta$ 的边缘概率密度为:

$f(\theta) = \int_{0}^{2\pi } f(\theta, \phi)d\phi = \int_{0}^{2\pi }\frac{\sin \theta}{2\pi}d\phi = \sin \theta\\$

再得到 $\phi$ 的条件概率密度为:

$f(\phi |\theta) = \frac{f(\theta, \phi)}{f(\theta)} = \frac{1}{2\pi}\\$

$\phi$ 的概率密度在 $\theta$ 确定时是固定的, 这和我们的直觉是相同的. 接下来来计算相应的概率分布函数:

$F(\theta) = \int_{0}^{\theta} \sin t dt = 1 - \cos\theta\\ F(\phi|\theta) = \int_{0}^{\phi} \frac{1}{2\pi} dt = \frac{\phi}{2\pi}$

求相应的反函数, 并将 $1 - \xi$ 替换为 $\xi$ , 得到:

$\theta = \arccos \xi_1\\ \phi = 2\pi \xi_2$

将结果用直角坐标系来表示:

$x = \sin\theta \cos \phi = \cos(2\pi \xi_2)\sqrt{1 - \xi_1 ^2}\\ y = \sin\theta \sin \phi = \sin(2\pi \xi_2)\sqrt{1 - \xi_1 ^2}\\ z = \cos \theta = \xi_1$

(3) 随机单位球面采样

推导过程和上面的几乎一模一样, 这里不再赘述. 最终结果为:

$x = \sin\theta \cos \phi = \cos(2\pi \xi_2)\sqrt{1 - z ^2} = \cos(2\pi \xi_2)\sqrt{\xi_1(1 - \xi_1)}\\ y = \sin\theta \sin \phi = \sin(2\pi \xi_2)\sqrt{1 - z ^2} = \sin(2\pi \xi_2)\sqrt{\xi_1(1 - \xi_1)}\\ z = \cos \theta =1 - 2 \xi_1$

(4) 随机单位圆采样

一个常见的错误是随机取半径, 随机取角度, 使用 $r = \xi_1, \theta = 2\pi\xi_2$ 来采样. 这样得到的结果会使得在圆的中心区域概率比边缘部分要高.

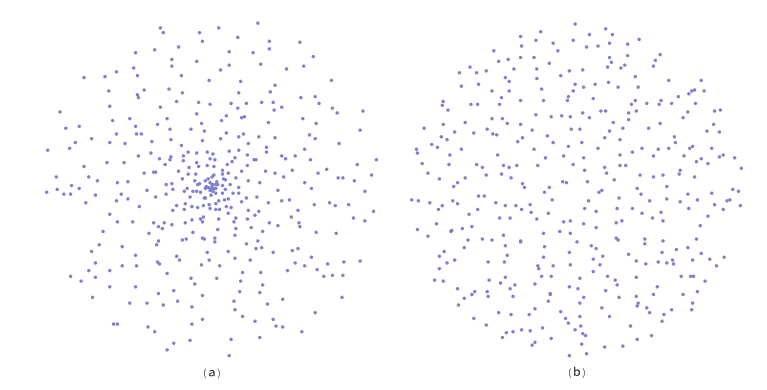
在单位圆上均匀采样时, 关于面积的概率密 $f(x, y)$ 是个常数, 可解得 $f(x, y) = 1 / \pi$ . 转换为极坐标系下得表示为 $f(r, \theta) = r / \pi$ . 使用和前面一样得推导过程得:

$f(r) = \int_{0}^{2\pi} f(r, \theta) d\theta = \int_{0}^{2\pi} \frac{r}{\pi} d\theta = 2r\\ f(\theta|r) = \frac{f(r, \theta)}{f(r)} = \frac{1}{2\pi}$

在 $r$ 确定时, 因为圆的对称性, $f(\theta|r)$ 是个固定常数. 进一步计算分布函数并取反函数可求得:

$r = \sqrt{\xi_1}\\ \theta = 2\pi \xi_2$

另外一种方式是使用正方形随机采样, 然后同心映射到圆上.

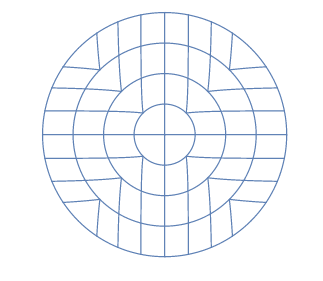
其中一个1/8部分的映射公式为:

$r = x\\ \theta = \frac{y}{x} \frac{\pi}{4}$

另外七个部分的映射公式可用相似的方式得到.

(5) 单位半球面余弦权重采样

求解图形学中的渲染方程时, 许多BRDF方程都是和夹角余弦相关的, 因此按照余弦采样是很有必要的. 即 $p(\omega) \propto \cos \theta$ , 求解概率密度为:

$\int_{H^2}^{} p(\omega) = 1\\ \int_{0}^{2\pi} \int_{0}^{\frac{\pi}{2}} c \cos \theta sin\theta d\phi = 1\\ c = \frac{1}{\pi}\\ f(\theta, \phi) = \frac{\cos \theta \sin \theta}{\pi}$

这样, 我们就可以继续使用上面的方式来推导出结果.

不过这里要介绍下Malley方法的实现, Malley方法就是先在单位圆上随机采样, 然后将单位圆上的点作为半球面上点的投影, 来得到半球面上的点.

下面我们来验证一下这种方式的正确性:

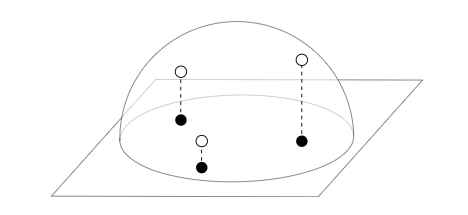
已知单位圆上随机采样的点极坐标为 $(r, \phi)$ , 概率密度为 $f(r, \theta) = r / \pi$ . 单位半球面上对应的点极坐标系为 $(\theta, \phi)$ , 两个坐标的关联为 $r = \sin \theta$ . 这样得到雅可比矩阵为:

$\begin{pmatrix} \cos \theta & 0\\ 0& 1\\ \end{pmatrix}\\$

行列式值为 $|J_M| = \cos \theta$ , 变换概率密度分布得:

$f(\theta, \phi) = f(r, \theta) \cos \theta = \frac{r}{\pi} \cos \theta =\frac{\cos \theta \sin \theta}{\pi} \\$

刚好符合上面我们想要得概率密度函数, 这样就可以从单位圆采样得到单位半球面上得采样.

其余的在锥形区域, 三角形, 长方形区域随机采样的过程和结果都是类似的, 这里不再给出. 这样我们可以随意按照自己想要的概率密度进行随机数采样, 下一篇会讲述如何使用随机数来实现蒙特卡洛积分.

编辑于 2020-08-31

看懂蒙特卡洛积分(一) 概率分布变换与随机采样

概率论基础

随机值采样

概率分布变换

二维随机变量采样

文章被以下专栏收录

实时渲染学习笔记

推荐阅读

看懂蒙特卡洛积分(二) 蒙特卡洛估计与重要性采样

低差异序列（二）- 高效实现以及应用

程序媛转TA之理论篇十三：蒙特卡洛方法

渲染方程与蒙特卡罗积分与重要性采样

4 条评论