多维随机变量函数的分布

coffee刚开始学习这一部分内容的时候，感到有些吃力，应该是大多数同学都有的感受，不过随着coffee啃教材啃题目多了，有了“山重水复疑无路，柳暗花明又一村”的感觉。现在coffee结合教材上的知识点，将自己的总结分享出来。这篇文章的结构是先给出几个重要的结论，再结合几个例题给出解决一般问题的方法。

这里讨论的多维随机变量，可分为离散型和连续型的，因而其函数就有三种组合：仅有离散型、仅有连续型、离散型和连续型的组合。

对于多维离散型随机变量的函数，若所给的是多维离散型随机变量的分布列，那么一般情况下根据该分布列和函数关系即可求出，这类问题较为简单，不做过多阐述。

离散场合下的卷积公式

我们首先定义分布的可加性：如果若干个属于同一类分布的独立随机变量的和的分布仍属于此类分布，称满足这样性质的分布具有可加性。

这里有两个特殊的离散型随机变量，二项分布和泊松分布，它们是具有可加性的。这一结论的证明需要引入离散场合下的卷积公式（这里的卷积是指，寻求两个独立随机变量和的分布的运算）：

设随机变量 是两个属于同一类分布的独立的离散型随机变量，设 的取值范围的交集为 ，记 ，则 .

这一结论是显然的，因为是独立的。不过要注意的是，上述的“属于同一类分布的独立的离散型随机变量”并不是“独立同分布”，这两个概念要严加区分。“同分布”意味着两随机变量服从同一个分布，即分布的参数要全部一致，而“同一类分布”并不意味着分布的参数要相同。

二项分布和泊松分布的可加性的证明详见教材，这里仅给出结论：

二项分布的可加性：

若随机变量 ，且 与 相互独立，则 。这个性质可以推广到有限个随机变量的场合： 。此即说明服从二项分布 的随机变量可以分解为 个相互独立的服从两点分布 的随机变量之和。

泊松分布的可加性：

若随机变量 ，且 与 相互独立，则 。这个性质可以推广到有限个随机变量的场合： 。

连续场合下的卷积公式

设 和 为两个相互独立的连续随机变量，其密度函数分别为 和 ，则其和 的密度函数为：

由此公式可以得到一些连续型随机变量分布的可加性：

正态分布的可加性：

设 ，且 与 独立，则 。这个结论可以推广到有限场合：任意 个相互独立的正态变量的线性组合仍服从正态分布：若 ，对于任意不全为零的常数列 ， .

伽玛分布的可加性：

设 ，且 与 独立，则 。这个结论可以推广到有限个尺度参数（ ）相同的场合：任意 个相互独立的尺度参数（ ）相同的伽玛变量的和仍服从伽玛分布：若 ， 则 .

又因为

（由此可推出 ）

结合伽玛分布的可加性，有：

1. 个独立同分布的指数变量之和为伽玛变量：

若 ，且 独立，则 .

2.卡方分布具有可加性：

若 ，且 独立，则 .

在概率论中，我们用“ ”这个式子来定义卡方分布；而在数理统计中，我们将给出卡方分布的构造定义：若 独立同分布于 ，则 ，记 服从自由度为 的卡方分布。事实上，我们可以利用求分布函数的方法证得：若 ，则 。那么我们可以这样理解卡方分布的“自由度”的这个概念：因为 可以看做是由 个自由的（独立）正态变量的平方所组成的。

至此我们给出了所有具有可加性的随机变量。

最大值、最小值分布

记 为 个相互独立的随机变量，且 。

1.

记 ，求 的分布，即最大值分布。

这种较为抽象的问题一般都从定义出发。求一个随机变量的分布，那就从它的分布函数出发，分布函数唯一决定了该分布（私以为这也是分布函数的名称来源）。根据分布函数的定义，不难得到：

，再对两边关于 求导，即得 .

特殊情况：若 独立同分布（不论离散或连续），则：

对该特殊情况进一步地，若 为连续型随机变量，则对上式两边关于 求导，有：

注意，上式中左边的 和右边的 要加以区分。

2.

记 ，求 的分布，即最小值分布。

按照上面最小值分布求解的思想，不难得到：

，再对两边关于 求导，即得 .

特殊情况：若 独立同分布（不论离散或连续），则：

对该特殊情况进一步地，若 为连续型随机变量，则对上式两边关于 求导，有：

注意，上式中左边的 和右边的 要加以区分。

对于该特殊情况，指数分布有一个很好的性质：

若 独立同分布，服从于 ，则

这个结论也很容易理解，我们知道指数分布往往与“寿命”有关，譬如电子器件的工作寿命，现设有一批同质的电子器件，设其工作寿命的期望为 ，则其工作寿命 。将这些电子器件串联起来，电路正常运行当且仅当所有电子器件正常运行，这个回路的工作寿命取决于正常运行时间最短的那个电子器件，记这个回路的工作寿命 。直观上容易理解，回路的工作寿命的期望为 ，从而 。

3.

设 独立同分布，记 ，求 的分布，即最大值与最小值的差的分布。

关于这类问题的求解，只需注意到有以下等式：

则 。若 为离散型随机变量，由于 独立同分布，根据对称性有， ，再结合 的分布列即可求得。若 为连续型随机变量，需画出满足条件的积分区域，确定好积分上下限后做积分求得分布函数，对其关于 求导得概率密度函数，具体问题具体分析，这里举一个例子。

e.g.1

设 独立同分布的 的概率密度函数如下：

求 的分布。

解：

当 时， ；

当 时，积分区域如下图阴影部分：

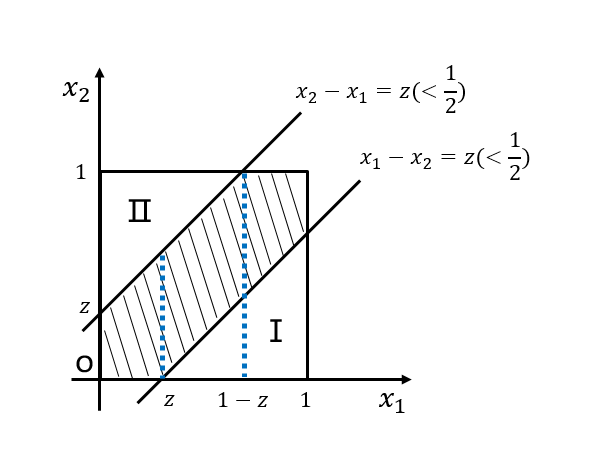
对该区域分三段进行积分：

当 时，积分区域如下图所示：

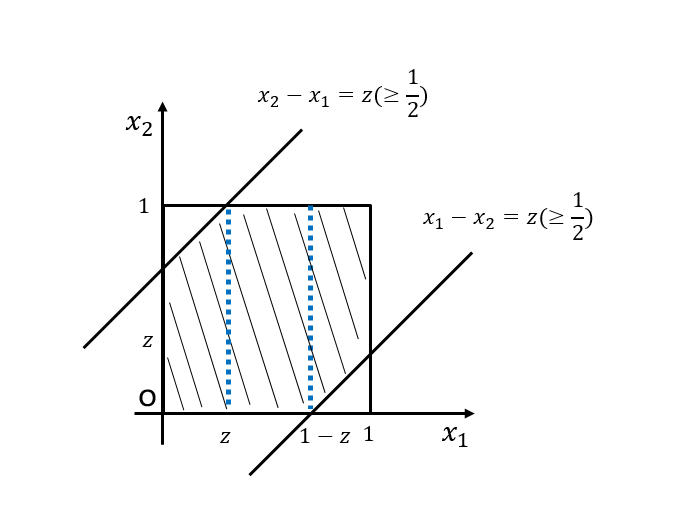
对该区域分三段进行积分：

但读者若自行尝试计算上面两个积分，会发现它们的计算非常繁琐，因而上述简单粗暴的方式只是提供一种思路。若利用“正难则反”的思想，则可以很容易地计算出结果：

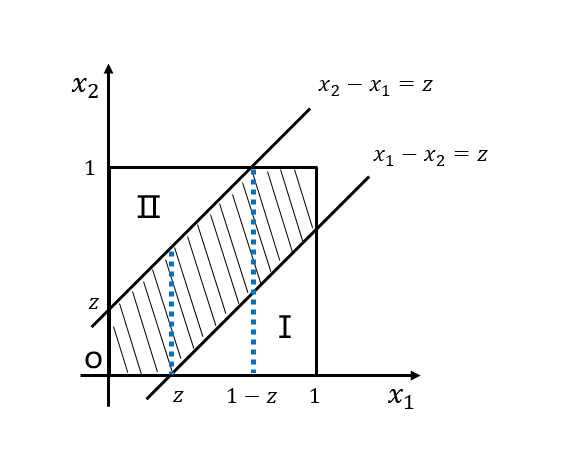
不难看出，上图中Ⅰ和Ⅱ两部分面积相等，又由于两变量概率密度函数相同，很容易可以求出：

求导即得：

当 时， .

综上所述：

这道题也可以利用下面要介绍的变量变换法求解，请读者自行尝试。

变量变换法

设二维随机变量 的联合密度函数为 ，若函数 有连续的偏导数，且存在唯一的反函数 ，该变换的Jocobi行列式 。若 ，则 的联合密度函数为 。

这个方法实际上是二重积分的变量变换法。我们知道二维随机变量的在某范围内的概率值对应的就是对概率密度函数在有利于条件的区域上的积分，也即二重积分（私以为这就是概率密度函数的由来，联系数学分析的二重积分，我们求的是曲顶柱体的体积，其实曲顶柱体的高度就是这里的概率密度函数对于的值）。因而可以利用二重积分中的变量变换法将复杂区域转化为简单区域，其中Jocobi行列式的绝对值就表示两区域面积的比例。

由变量变换法的思想可以导出两种特殊类型随机变量的概率密度函数：

1.积的公式

设随机变量 相互独立，其密度函数分别为 ，则 的密度函数为：

2.商的公式

设随机变量 相互独立，其密度函数分别为 ，则 的密度函数为：

下面举两个例子来巩固一下对上述公式的理解和应用。

e.g.2

设 相互独立，且 ，求 的密度函数。

解：

方法一：分布函数法

（ 分布函数是求解分布问题的最根本的解法，我们首先利用该方法来求解这个问题）

作曲线簇 ，因 ， ，易知临界点为 。如图所示（其实这里应该画出三维坐标轴来确定积分区域，但是教材偷懒了！因而我也就偷懒了……）：

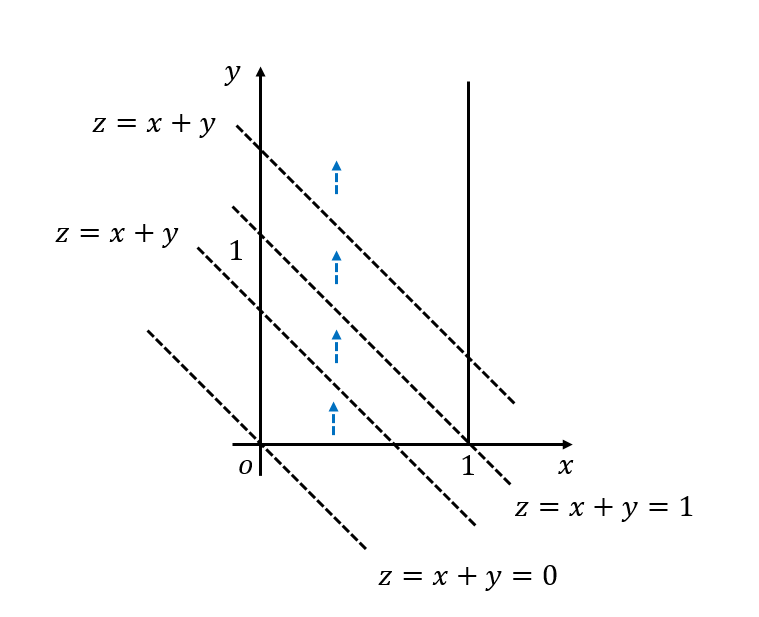
对于一个固定的 ，概率密度函数非零的区域为虚线上方的区域（箭头所指）。

当 时， ；
当 时，
当 时，

综上所述：

方法二：卷积公式

二.1：考虑对 积分：

作曲线簇 ，因 ，易知两条临界直线为： ，如图：

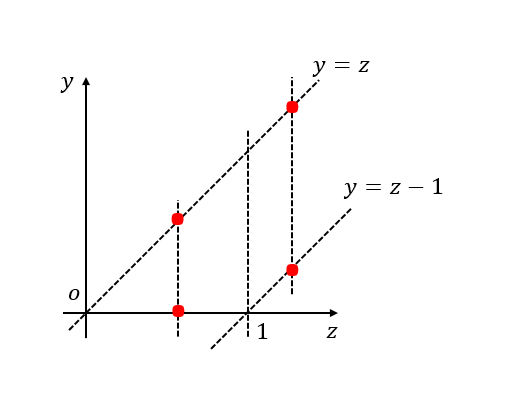
当 时， ；
当 时，
当 时，

综上所述：

二.2：考虑对 积分：

作曲线簇 ，因 ，易知两条临界直线为： ，如图：

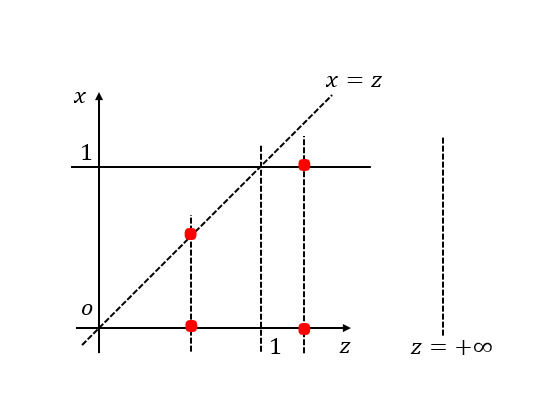
当 时， ；
当 时，
当 时，

综上所述：

上面利用了两种方法（实际上是三种）来求解这个问题。

实际上，变量变换法对一维和高维都成立，下面看一个一维的例子。

e.g.3

设随机变量 ，求 的分布。

方法一：分布函数法

当 时， ；当 时，有：

两边关于 求导，有：

综上所述：

方法二：变量变换法

做变换： ，则

则

当 时， ；当 时：

综上所述：

可以看出 。

下面我们看一个非常容易出错的题目。

e.g.4

设随机变量 独立同分布于 ，求 的联合密度函数 。

显然这里需要用到变量变换法。最直接的就是利用题设条件做变换：

直观上考虑到通过解这个变换的逆变换再求Jocobi行列式会比较复杂，因而我们利用这个性质：

即：

由于 独立同分布，则当 时，

我们算出来了 ，而且自作聪明，完全没有求那个看似复杂的逆变换，并且在上面的计算中巧妙地利用了等式： ，沾沾自喜。然而很遗憾的是，这个答案是错的。究其原因在于没有注意到变量变换法要求所做的变换存在唯一的反函数。所以下面我们就老老实实求一下逆变换，看看究竟错在哪。

求解逆变换的过程我就不写了，直接给出逆变换：

可以看出反函数不唯一，因此要分开讨论。

当我们研究(1)时，可以看到 ，而 可以取遍 ，这样确定的 区域可以使 取遍 、 取遍 。同样地，当我们研究(2)时，可以看到 ，而 可以取遍 ，这样确定的 区域可以使 取遍 、 取遍 。这样我们将区域分两部分讨论，使得变化前后所有可能取得的情况都得到了讨论。从而：

可以看到这个结果是之前的两倍。

离散型和连续型的结合

这里仅举一个例子。

e.g.5

已知 ， ，求 的分布。

离散型和连续型的结合是我们从未见过的类型，要求分布，就从分布的定义出发，即从分布函数出发。

解：

对上式两边关于 求导：

因

上式可进一步化简，此处省略。

综上所述：