【DRL-7】Distributional DQN: Quantile Regression-DQN

论文

这篇文章在上一篇的基础之上做了扩展，作者还是同一拨人。

提要：QR-DQN是对DQN的扩展，是model-free，off-policy，value-based，discrete的方法。

听说点赞的人逢投必中。

在这之前你需要了解一些分位数和分位数回归的知识，建议先读

石川：用 Quantile Regression 分析变量相关性444 赞同 · 25 评论文章

同时还有一些Bellman算子的知识，建议先读

Frank Tian：用Bellman算子理解动态规划150 赞同 · 15 评论文章

首先我们来介绍一个数学概念，Wasserstein距离。

Wasserstein距离度量两个概率分布之间的距离，（狭义的）定义如下：

$W(P,Q)=\underset{\gamma \in \mathrm{\Pi }}{min}\sum _{x_p,x_q}\gamma (x_p,x_q)\Vert x_p-x_q\Vert$

直接看这个式子可能过于抽象了，因为它和我们熟悉的度量不一样，它好像不是确定性的，而是带有一个 $min$ 。

这里的Wasserstein距离又叫推土机距离，看下面的图，你就能很形象的理解Wasserstein距离。

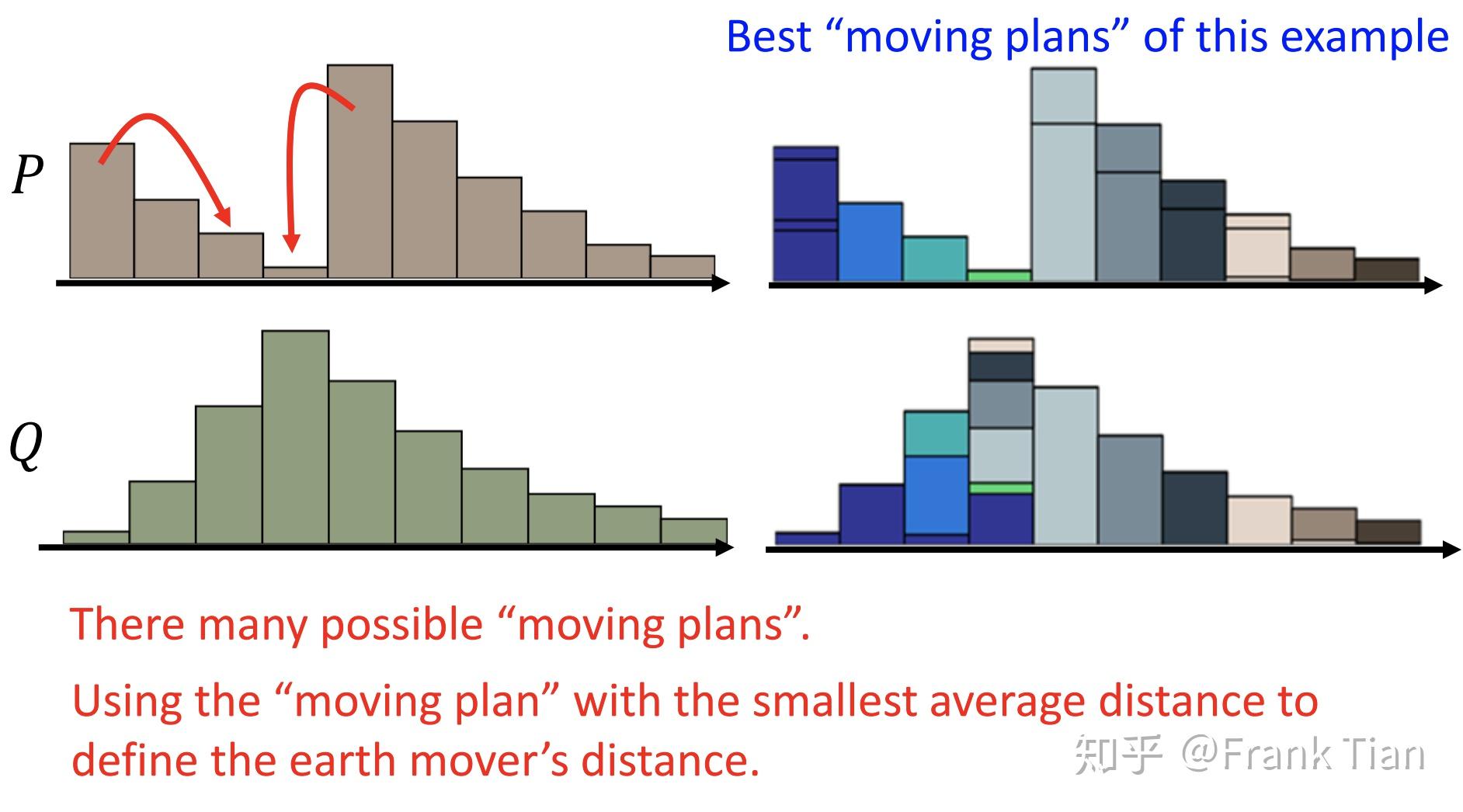
它的意思是，将一个分布转变为另一个分布，所需要移动的最少的“土”的量。

注意，因为是分布，概率的和为1，也就是说“土”的总量是相同的。同时，这个移动的量是指“土”的“距离*数量”。

可以看到，又很多种移动的方案，而Wasserstein距离指的是最少的那种，当然可能有多个方案都是最少，但是这不重要，重要的是移动的值。

我们把每一种移动方案叫做一个moving plan，用下面的矩阵表示：

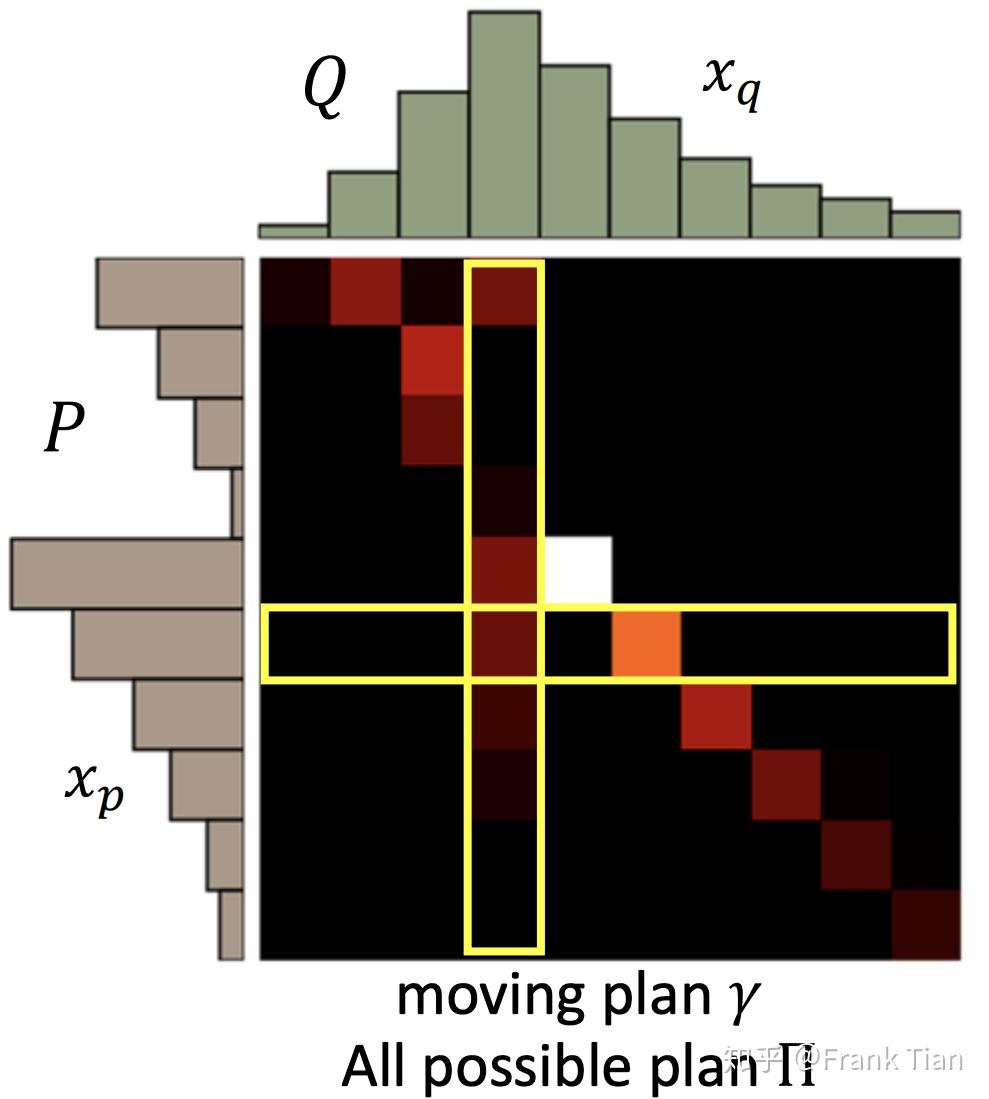
上面的矩阵代表了将P移动到Q的moving plan，明暗程度代表大小。

用 $\gamma$ 代表一个moving plan， $\mathrm{\Pi }$ 代表moving plans的全集。

$\underset{\gamma \in \mathrm{\Pi }}{min}$ 的意思就是，从 $\mathrm{\Pi }$ 中挑选出那个能让“移动土的量”最少的方案。

然而上述的定义只算是一个特例，标准的Wasserstein Metric的定义更为复杂，如果我有两个分布 $U,Y$ ，那么它们的p-Wasserstein Metric为

$W_p(U,Y)={\left({\int }_0^1{|F_Y^{-1}(\omega )-F_U^{-1}(\omega )|}^{p}d\omega \right)}^{1/p}$

其中

$F_Y^{-1}(\omega ):=inf\{y\in \mathbb{R}:\omega \le F_Y(y)\}$

$F_Y(y)=\mathrm{Pr}(Y\le y)$

当 $p=1$ 的时候，上面的公式就退化成为我们最开始看到的推土机距离。

当 $p=1$ 的时候这个式子还是容易理解的，这里的 $F_Y(y)$ 就是 $y$ 的CDF函数，而 $F_Y^{-1}(\omega )$ 可以理解为计算 $P_Y$ 的 $w$ 分位数。

而 $W_p(U,Y)$ 的表达式，则是将这个代表分位数的 $w$ 从 $0$ 到 $1$ 积分。

下图形象的描述了 $p=1$ 情况下的Wasserstein Metric，这不过这个定义是连续的，刚才的那个是离散的。

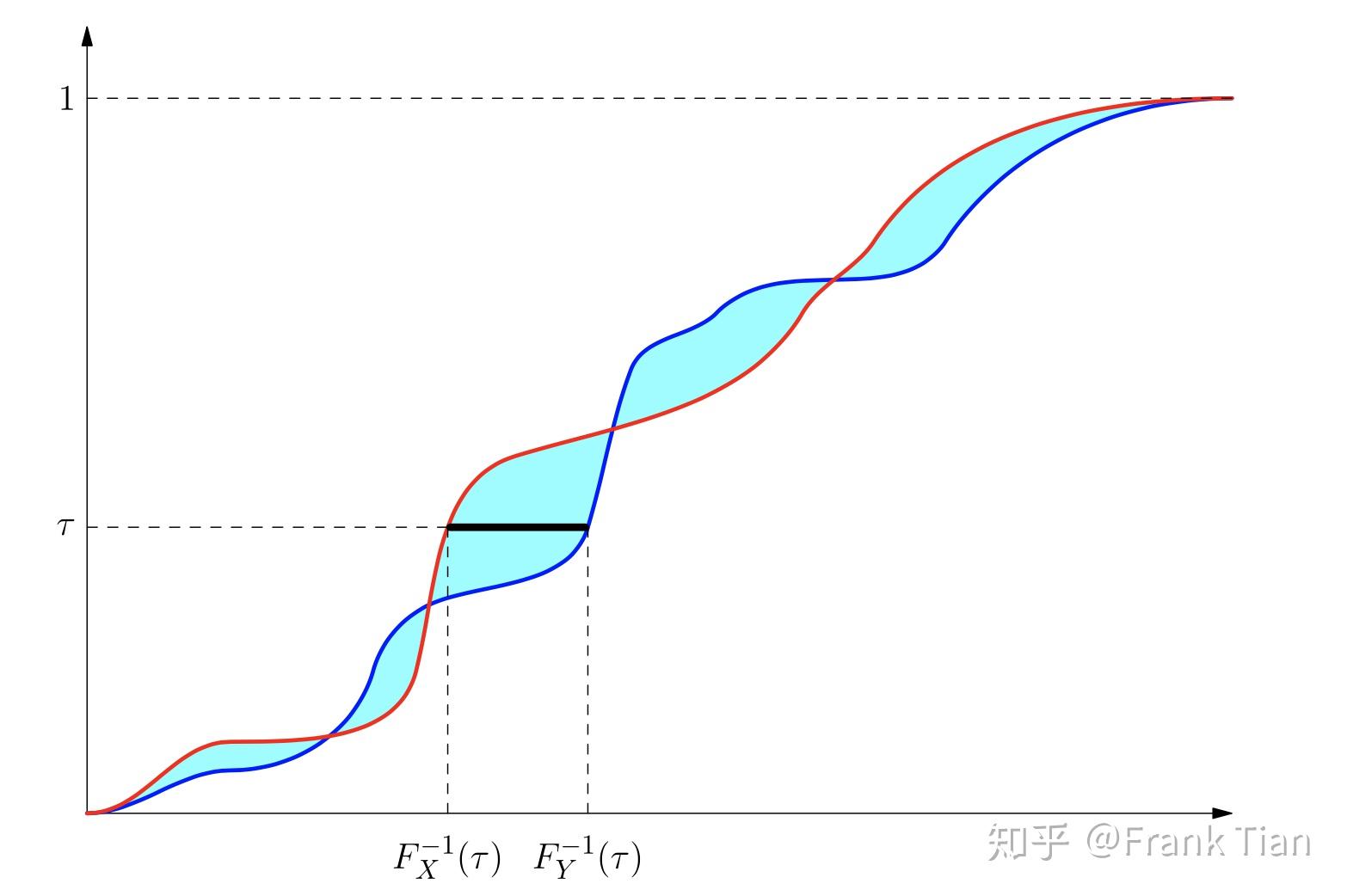
上图中红色和蓝色的线分别是 $P_X$ 和 $P_Y$ 的CDF函数，对于某一个分位数 $\tau$ ，我们可以计算得到两个值，分别是 $F_X^{-1}(\tau )$ 和 $F_Y^{-1}(\tau )$ 。

它们的差值的绝对值就是上图中黑线的长度，把这个长度积分就是青色部分的面积，这就代表了两个分布的差异。

接下来我们步入正题，在上一篇文章

Frank Tian：【DRL-6】Distributional DQN: C51201 赞同 · 19 评论文章

中，我们说到，可以用 $Z(x,a)$ 表示值分布，准确的说，它可以表示成下面的形式

$Z:\mathcal{X}\times \mathcal{A}\to \mathcal{P}(\mathbb{R})$

接下来我们定义 $Z$ 这个函数所在的空间 $\mathcal{Z}$

$\mathcal{Z}=\{Z:\mathcal{X}\times \mathcal{A}\to \mathcal{P}(\mathbb{R})|\mathbb{E}[|Z(x,a){|}^p]<\mathrm{\infty },\mathrm{\forall }(x,a),p\ge 1\}$

在Bellman算子的那篇文章中，我们说我们如果想要证明某个方法能否收敛，需要证明它对应的算子有唯一的不动点，也就是要证明这个算子是$\gamma -\text{ contraction}$的。

在 $Q(s,a)$ 的例子中，我们证明bellman operator是$\gamma -\text{ contraction}$的，即证明

$\mathrm{dist}({\mathcal{T}}^{\pi }{Q}_1,{\mathcal{T}}^{\pi }{Q}_2)\le \gamma \mathrm{dist}(Q_1,Q_2)$

这里的 $\text{dist}$ 表示直径，也就是这两个函数 $Q_1$ 和 $Q_2$ 的最远距离。

在值函数的例子中，这个 $\text{dist}$ 的定义很简单，就是 $\Vert Q_1-Q_2{\Vert }_{\mathrm{\infty }}$ ，也就是它们差值的无穷范数。

注意，这里我们其实用到了两个度量，一个是“差值”，一个是“无穷范数”。第一个度量取决于你的实际用途，而第二个度量是不可避免的，因为它定义了“直径”。

在值分布的例子中，我们也要证明bellman operator是$\gamma -\text{ contraction}$的，那么我们需要找到合适的度量。

这里的度量就是Wasserstein Metric。

于是，在这个例子中， $\text{dist}$ 就变成了

${\overline{d}}_p(Z_1,Z_2):=\underset{x,a}{sup}{W}_p(Z_1(x,a),Z_2(x,a))$

其中的 $\underset{x,a}{sup}$ 发挥了无穷级数的作用，而 $W_p$ 发挥了第一个度量，也就是差值的作用。

那么，要证明值分布的情况下算法依旧收敛，只需要证明对于任意的 $Z_1,Z_2\in \mathcal{Z}$ ，有

${\overline{d}}_p({\mathcal{T}}^{\pi }{Z}_1,{\mathcal{T}}^{\pi }{Z}_2)\le \gamma {\overline{d}}_p(Z_1,Z_2)$

这里我们就不做证明了，具体证明在论文的附录中有。

上面的说明给值分布的算法提供了理论保证，但是一开始作者们并没有想到合适的方法模拟Wasserstein Metric这个过程，于是提出了使用KL散度做近似的想法。

实际上，基于这个想法提出的C51算法确实效果不错。

然而，紧接着作者们又提出了更“正统”的算法QR-DQN，它继承了最开始的理论想法。

首先，我们要做的是改变“分布”的表现形式。

$Z(x,a)$ 是$Z:\mathcal{X}\times \mathcal{A}\to \mathcal{P}(\mathbb{R})$ 的函数，它的输出是一个分布 $\mathcal{P}(\mathbb{R})$ 。

我们一开始是用 $N$ 个atoms $\{z_0,z_1,\cdots ,z_{N-1}\}$ 作为基准，再用 $N$ 个离散的分布 $\{p_0,p_1,\cdots ,p_{N-1}\}$ 来描述这个分布。

这种形式用来计算KL散度是极好的，但是不适合计算W度量，现在我们介绍另外一种，是用分位数描述的方法。

其实也很直觉，就是按照这个分布的CDF的 $y$ 轴，把它均等的分成 $N$ 分，例如下面的是分布的PDF的 $y$ 轴，我们把它分成10等分

那么自然就会得到10个 $\hat{\tau }$ ，这10个 $\hat{\tau }$ 就定义了10个分位数

${\hat{\tau }}_i=\frac{2(i-1)+1}{2N},i=1,\dots ,N$

分位数是下图的小红点

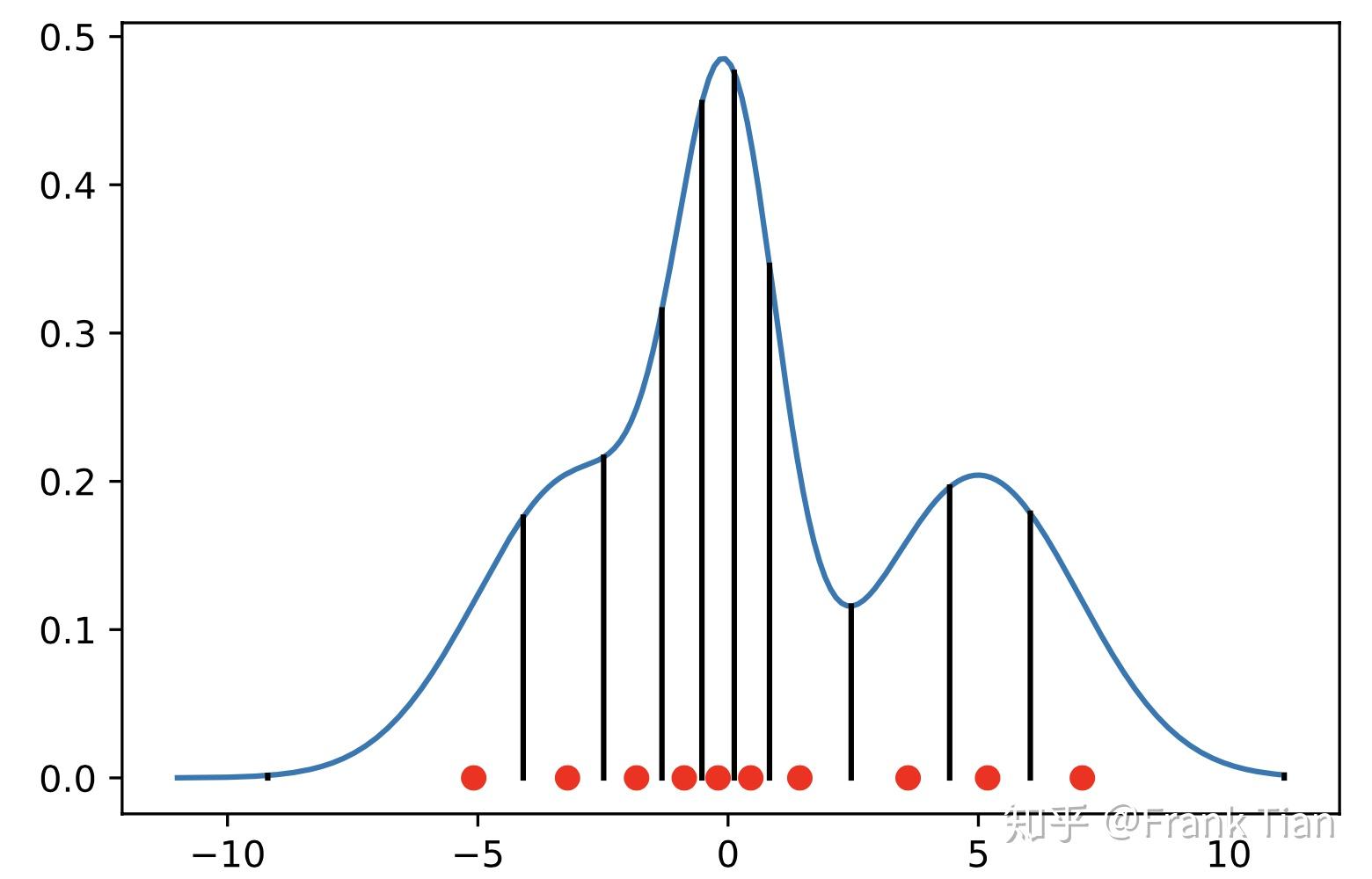
于是，我们现在只需要记录 $N$ 个分位数的位置，就可以描述整个分布了。

接下来，我们如何去学习出这 $N$ 个分位数呢？

还记得在C中，我们设计了一个神经网络 $Z$ ，它的输入是状态 $s$ ，输出是一个矩阵，矩阵的每一行代表一个动作的 $N$ 个概率，分别是 $\{p_0,p_1,\cdots ,p_{N-1}\}$ 。

而学习出分位数，就需要分位数回归的知识了。

我在这里再简单叙述一下。

在传统的回归中，我们想要的是，对于一个自变量 $x$ ，条件概率 $p(y|x)$ 的期望，因此我们的损失函数是

$L_{MSE}=\underset{\beta }{min}\sum _i^n{(y_i-\mu (x_i,\beta ))}^2$

其中 $\beta$ 就代表了模型的参数。这是很显然的，因为让MSE最小的点正好是期望。

如果我们想求 $p(y|x)$ 的中位数呢？那就不能再用MSE了，而是应该用MAE

$L_{MAE}=\sum _i^n|y_i-\xi (x_i,\beta )|$

上面的式子也可以表示为

$L_{MAE}=\sum _{i:y_i\ge \xi (x_i,\beta )}(y_i-\xi (x_i,{\beta }_{\tau }))+\sum _{i:y_i<\xi (x_i,\beta )}(\xi (x_i,\beta )-y_i)$

这个式子的来历很简单，就是分类讨论了一下。

在训练的时候，也很容易求梯度

${\mathrm{\nabla }}_{\beta }{L}_{MSE}=\sum _i^n{\mathrm{\nabla }}_i$

其中 ${\mathrm{\nabla }}_i=\{\begin{array}{}1& i:y_i<\xi (x_i,\beta )\\ -1& i:y_i\ge \xi (x_i,\beta )\end{array}$

可以把梯度理解为将 $\xi (x_i,\beta )$ 往中间推的力量。

实际上，我们说中位数就是 $\tau =0.5$ 的分位数，求其他任意的分位数也很容易扩展了

$L_{\tau }=\sum _{i:y_i\ge \xi (x_i,{\beta }_{\tau })}\tau (y_i-\xi (x_i,{\beta }_{\tau }))+\sum _{i:y_i<\xi (x_i,{\beta }_{\tau })}(1-\tau )(\xi (x_i,{\beta }_{\tau })-y_i)$

这可以看作推的力量有了一个“加权“，使之不再正好往中间推，而是推向了某一个位置，这个位置正是由 $\tau$ 决定的。

梯度表示为

${\mathrm{\nabla }}_{\beta }{L}_{\tau }=\sum _i^n{\mathrm{\nabla }}_i$

其中 ${\mathrm{\nabla }}_i=\{\begin{array}{}1-\tau & i:y_i<\xi (x_i,{\beta }_{\tau })\\ -\tau & i:y_i\ge \xi (x_i,{\beta }_{\tau })\end{array}$

我们还可以换一种形式表示 $L_{\tau }$ ，令 ${\delta }_{\text{statement }}$ 表示

${\delta }_{\text{statement }}=\{\begin{array}{}1& \text{statement is ture}\\ 0& \text{otherwise }\end{array}$

于是

$|\tau -{\delta }_{y_i<\xi (x_i,\beta )}|=\{\begin{array}{ll}|\tau -1|=1-\tau & \text{ if }{y}_i<\xi (x_i,\beta )\\ \tau & \text{ if }{y}_i\ge \xi (x_i,\beta )\ge \theta \end{array}$

所以

$\begin{array}{rl}{L}_{\tau }& =\mathbb{E}[|y_i-\xi (x_i,{\beta }_{\tau })||\tau -{\delta }_{y_i<\xi (x_i,\beta )}|]\\ & =\mathbb{E}[{\rho }_{\tau }(y_i-\xi (x_i,{\beta }_{\tau }))]\end{array}$

其中

$\begin{array}{rl}{\rho }_{\tau }(u)& =|u||\tau -{\delta }_{u<0}|\\ & =u(\tau -{\delta }_{u<0})\end{array}$

因为 $|u|$ 在 $0$ 出不可导，我们可以把它换成其他函数，论文中使用的是

${\mathcal{L}}_{\kappa }(u)=\{\begin{array}{ll}\frac{1}{2}{u}^2& \text{ if }|u|\le \kappa \\ \kappa (|u|-\frac{1}{2}\kappa )& \text{ otherwise }\end{array}$

这个 $\kappa$ 可以看作另一个超参数，但是其实没有调节它的必要啦。

当 $\kappa =1$ 时

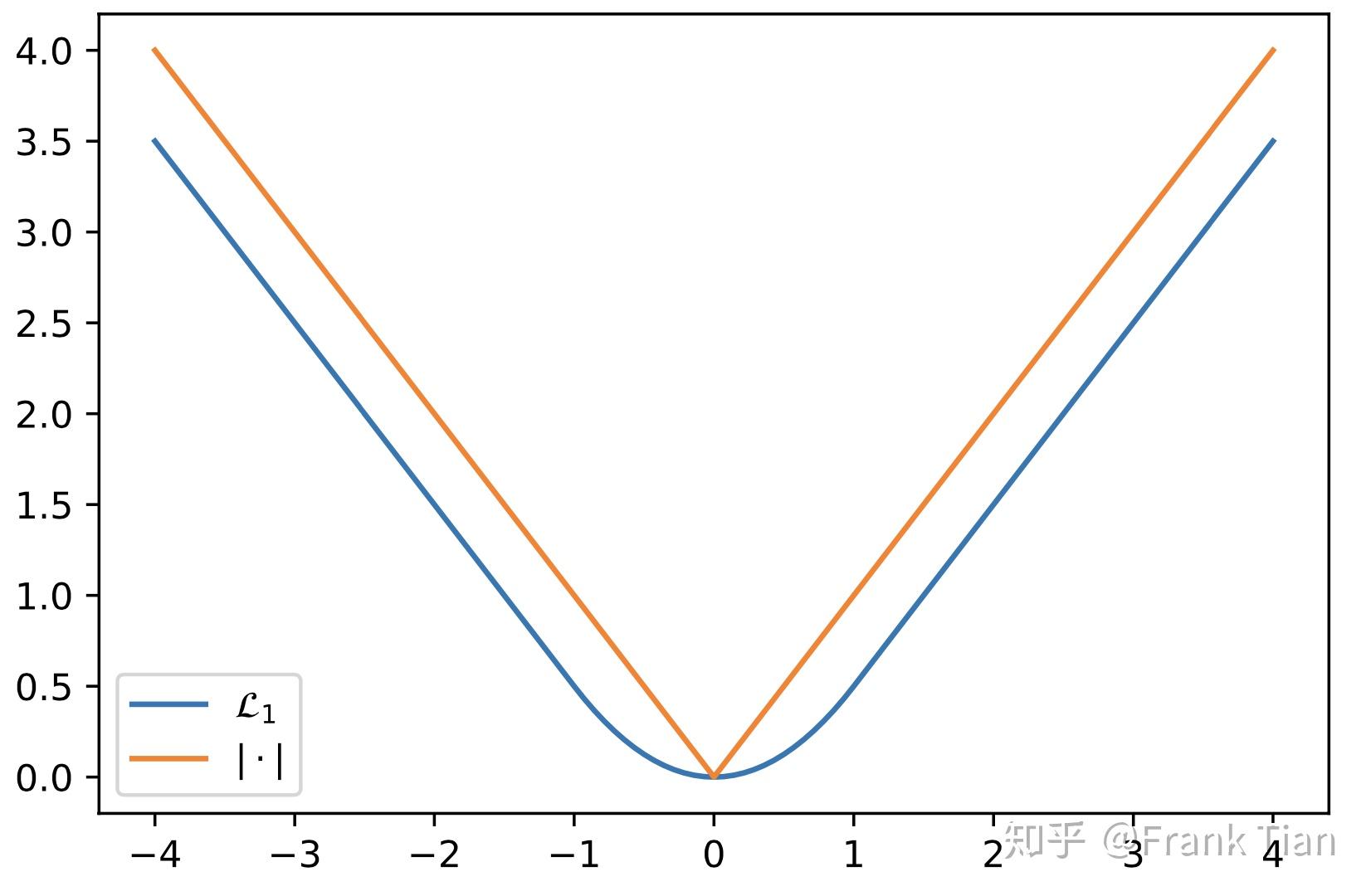
那么现在我们有

${\rho }_{\tau }^{\kappa }(u)={\mathcal{L}}_{\kappa }(u)|\tau -{\delta }_{u<0}|$

对比一下 ${\rho }_{\tau }^{\kappa }(u)$ 和 ${\rho }_{\tau }(u)$

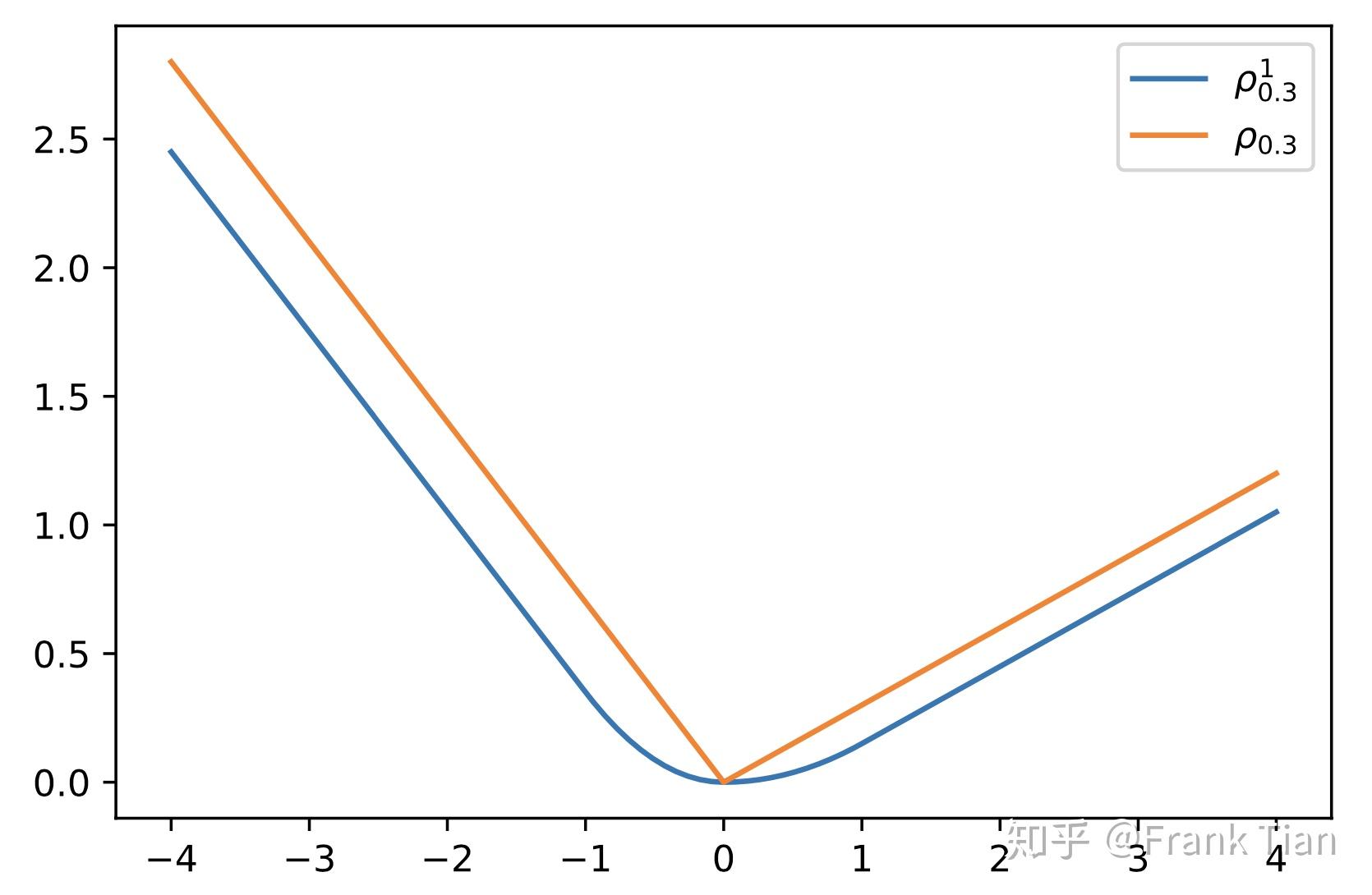
最终我们把损失函数定义为

$\begin{array}{r}{L}_{\tau }=\mathbb{E}[{\rho }_{\tau }^1(y_i-\xi (x_i,{\beta }_{\tau }))]\end{array}$

在QR-DQN中，神经网络是怎么定义的呢？

其实和C51的很像，也是输出一个矩阵，只不过每列不再是atoms对应的 $p_i$ 了，而是atoms的位置，也就是 $z_i$ ，因为在QR-DQN中atoms的概率是确定的，都是 $\frac{1}{N}$ 。

现在让我们看一下训练的过程。

首先我们从Buffer中采样出 $(s,a,r,s^{\mathrm{\prime }})$ ，接下来我们需要计算出 $a^{\ast }$ ，和C51的想法一样，我们依旧用 $Q(s,a)$ 来计算。

先算 $Q(s^{\mathrm{\prime }},a^{\mathrm{\prime }})$

$Q(s^{\mathrm{\prime }},a^{\mathrm{\prime }}):=\sum _j{q}_j{\theta }_j(x^{\mathrm{\prime }},a^{\mathrm{\prime }})$

挑出最大的作为 $a^{\ast }$

$a^{\ast }\leftarrow \arg \underset{a^{\mathrm{\prime }}}{max}Q(x,a^{\mathrm{\prime }})$

根据这个 $a^{\ast }$ 计算出分布 $Z(s^{\mathrm{\prime }},a^{\ast })$ ，我们设这个分布的atoms的位置表示为 $\{{\theta }_0^{\mathrm{\prime }},{\theta }_1^{\mathrm{\prime }},\dots ,{\theta }_{N-1}^{\mathrm{\prime }}\}$

那么目标分布表示为

$\mathcal{T}{\theta }_j^{\mathrm{\prime }}=r+\gamma {\theta }_j^{\mathrm{\prime }},i=0,\dots ,N-1$

这里的好处是不用再对齐了，因为我们的atoms的位置是可以改变的，而正是用这个变量来描述整个分布，自然没有对齐之说。

最关键的是，我们要让分布 $Z(s,a)$ 和目标分布 $r+\gamma Z(s^{\mathrm{\prime }},a^{\ast })$ 尽可能相似。

我们假设用 $\{{\theta }_0,{\theta }_1,\dots ,{\theta }_{N-1}\}$ 来描述分布 $Z(s,a)$ ，这其实就是 $N$ 个分位数。

那么描述目标分布的 $\{r+\gamma {\theta }_0^{\mathrm{\prime }},r+\gamma {\theta }_1^{\mathrm{\prime }},\cdots ,r+\gamma {\theta }_{N-1}^{\mathrm{\prime }}\}$ 就可以当作ground truth，也就是把他们看作 $\begin{array}{r}{L}_{\tau }=\mathbb{E}[{\rho }_{\tau }^1(y_i-\xi (x_i,{\beta }_{\tau }))]\end{array}$ 中不同的 $y_i$ 。

此外，我们并不是只有一个 $\tau$ ，我们有 $N$ 个 $\tau$ ，我们需要计算它们的损失函数的和，也就是

$\begin{array}{rl}{L}_{\beta }& =\sum _{i=1}^N{\mathbb{E}}_Y\left[{\rho }_{{\tau }_i}^1(Y-\xi (\beta {)}_i)\right]\\ & =\sum _{i=1}^N{\mathbb{E}}_{\mathcal{T}{Z}^{\mathrm{\prime }}}\left[{\rho }_{{\hat{\tau }}_i}^1(\mathcal{T}{Z}^{\mathrm{\prime }}-{\theta }_i)\right]\\ & =\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^N\left[{\rho }_{{\hat{\tau }}_i}^1(\mathcal{T}{\theta }_j^{\mathrm{\prime }}-{\theta }_i)\right]\end{array}$

其中

$\mathcal{T}{Z}^{\mathrm{\prime }}=r+\gamma Z(x^{\mathrm{\prime }},a^{\ast })$

而 ${\hat{\tau }}_i$ 就是用来决定 $N$ 个分位数的值

${\hat{\tau }}_i=\frac{2i+1}{2N},i=0,\dots ,N-1$

最后算法如下

我们来直观的感受一下QR-DQN做了什么。

假设我们现在可以画出 $r+\gamma Z(s^{\mathrm{\prime }},a^{\ast })$ ，它就是下图的红线

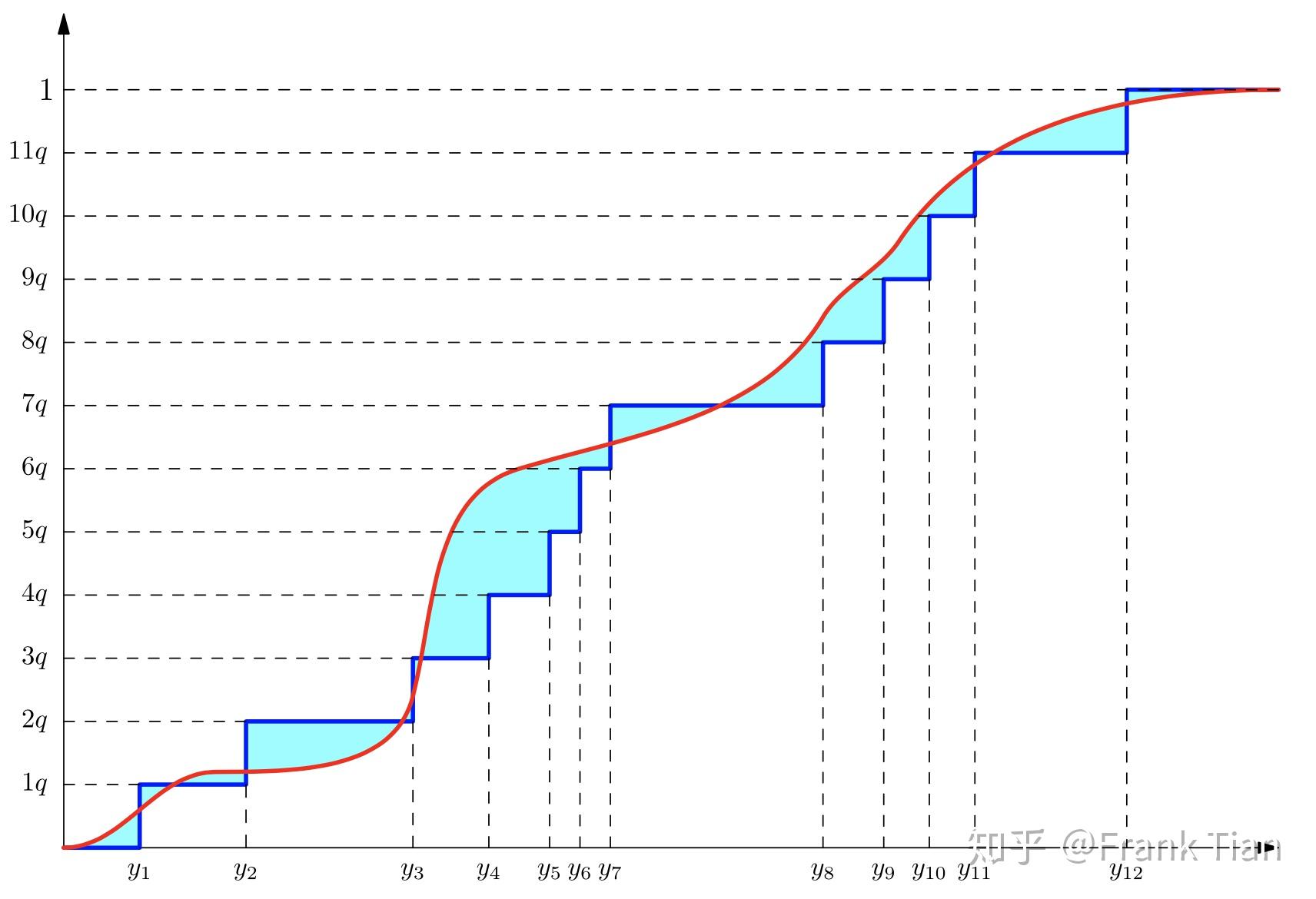
那么蓝色的线就是初始状态的 $Z(s,a)$ 。

从Distributional DQN定义的角度，我们希望什么呢？我们希望青色的面积更小。

那么QR-DQN希望什么呢？

它希望 ${\theta }_0$ 可以可以作为 ${\tau }_0$ 对应的分位数， ${\theta }_1$ 可以可以作为 ${\tau }_1$ 对应的分位数，以此类推。

如果做到了这一点，图像就会变成

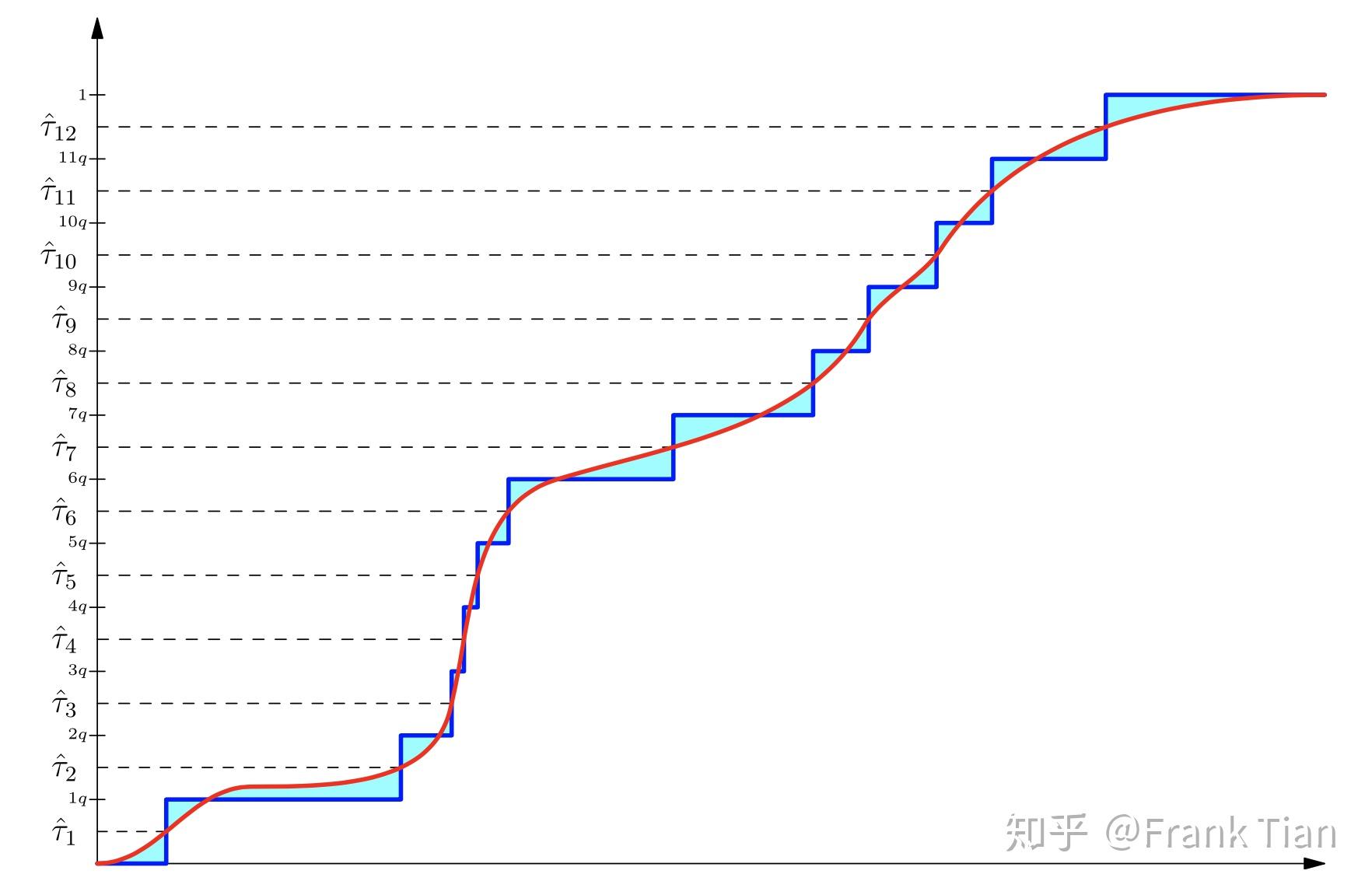
Amazing啊，青色这不就变少了。

如果我们调节超参数 $N$ ，让QR-DQN的分布描述的更细致，会变成

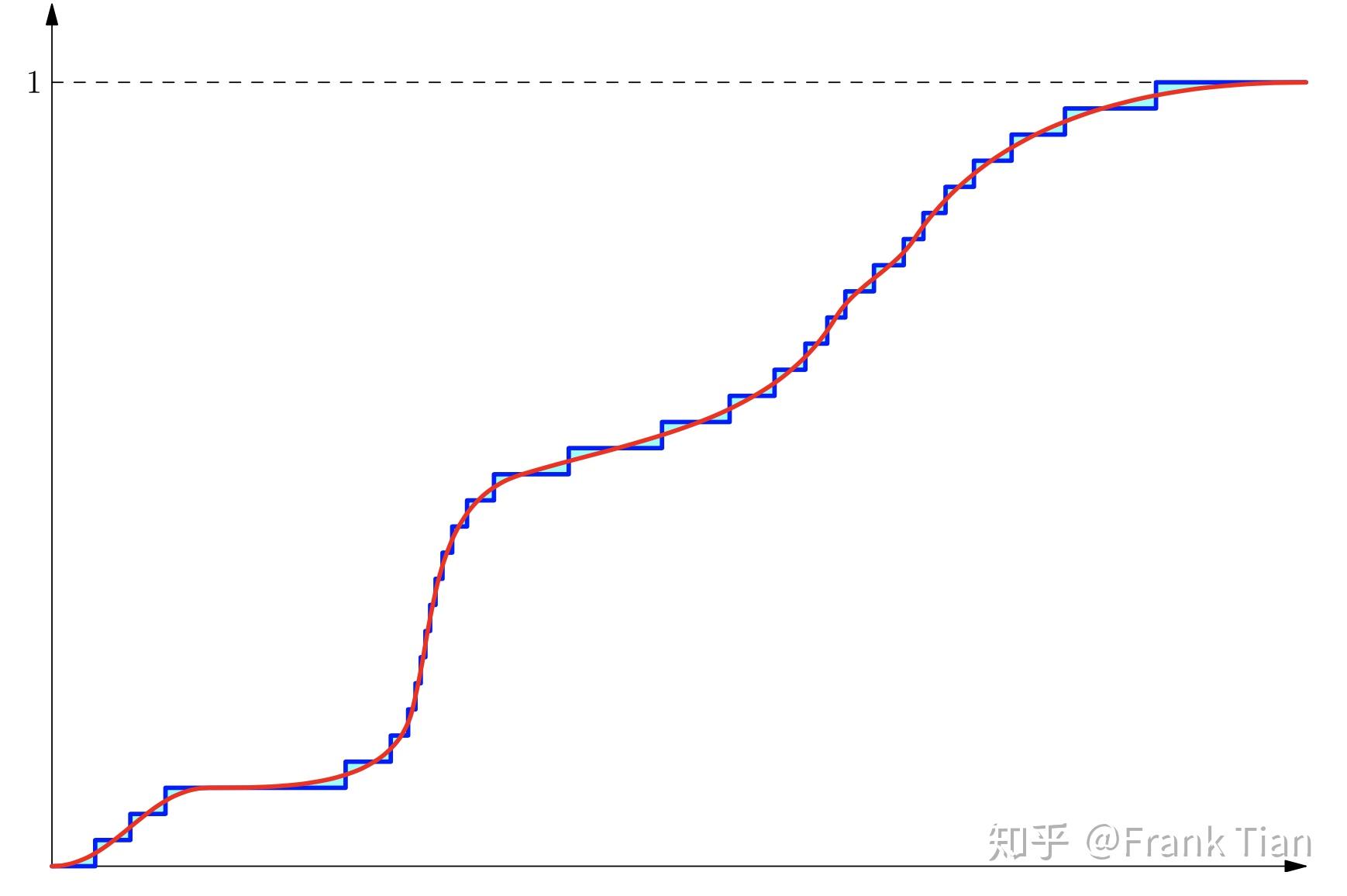
青色更少了。

本文参考自