【DRL-8】Distributional DQN: Implicit Quantile Nets

论文

提要：IQN是对DQN的扩展，是model-free，off-policy，value-based，discrete的方法。

听说点赞的人逢投必中。

在介绍IQN之前我们现在说说Risk-Sensitive Reinforcement Learning。

Risk-Sensitive强化学习指的是我们在针对相同的 $Z(s,a)$ 分布时，根据不同的偏好，应该做出不同的动作。

在以前的DQN中，这种事情是不肯呢个发生的，因为回想一下，我们是拿不到 $Z(s,a)$ 的分布的，我们用来评价每一个 $s,a$ 的信息只有 $Q(s,a)$ ，这只是一个实数。

还记得小学的数学题吗，两个打枪的运动员，一个均值很高但方差也很大，另一个均值没那么高但是实力稳定，在不同的情况下我们会选择不同的运动员。

比如如果你们国家的实力很菜，那就不如让第一个去，万一呢。

但是如果你们实力比较强，这时候讲究发挥稳定，这时候就应该派第二个去了。

这就是所谓的偏好，在不同任务，不同场景下，我们的偏好应该不同。

在DQN中，我们只能拿到一个 $Q(s,a)$ ，也就是 $\mathbb{E}[Z(s,a)]$ ，连方差都没有，自然没办法作出这种抉择。

我们把对待风险两种不同的态度成为risk-averse和risk-seeking，接下来，我们用一种正式的数学语言来描述它们。

描述这种偏好的公理被成为独立性，它有两个版本。

版本一

如果有两个随机变量 $X,Y$ ，我们相比 $Y$ 更偏好 $X$ ，写作 $X\succ Y$ ，那么这代表对任何随机变量 $Z$ ， $X$ 和 $Z$ 的混合都优于 $Y$ 和 $Z$ 的混合，这种“优于”表示为

$\alpha F_X+(1-\alpha )F_Z\ge \alpha F_Y+(1-\alpha )F_Z,\mathrm{\forall }\alpha \in [0,1]$

在这种情况下，我们可以找到一个效用函数 $U$ 来描述这种偏好，那么策略可以表示为

$\pi (x)=\underset{a}{\arg max}\underset{Z(x,a)}{\mathbb{E}}[U(z)]$

版本二

如果有两个随机变量 $X,Y$ ，我们相比 $Y$ 更偏好 $X$ ，写作 $X\succ Y$ ，那么这代表对任何随机变量 $Z$ ， $X$ 和 $Z$ 的混合都优于 $Y$ 和 $Z$ 的混合，这种“优于”表示为

$\alpha F_X^{-1}+(1-\alpha )F_Z^{-1}\ge \alpha F_Y^{-1}+(1-\alpha )F_Z^{-1},\mathrm{\forall }\alpha \in [0,1]$

在这种情况下，我们可以找到一个distortion risk measure $h$ 来描述这种偏好，那么策略可以表示为

$\pi (x)=\underset{a}{\arg max}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}z\frac{\mathrm{\partial }}{\mathrm{\partial }z}(h\circ F_{Z(x,a)})(z)dz$

可以证明，这两种表示是可逆的，也就是哪个方便按哪个来。

举个例子，在第一个版本中，如果 $U(x)=x$ ，那么策略就会变成

$\pi (x)=\underset{a}{\arg max}\underset{Z(x,a)}{\mathbb{E}}[z]=\underset{a}{\arg max}Q(x,a)$

在第二个版本中，如果 $h(x)=x$ ，那么策略就会变成

$\begin{array}{rl}\pi (x)& =\underset{a}{\arg max}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}z\frac{\mathrm{\partial }}{\mathrm{\partial }z}{F}_{Z(x,a)}(z)dz\\ & =\underset{a}{\arg max}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}z{P}_{Z(x,a)}(z)dz\\ & =\underset{a}{\arg max}\underset{Z(x,a)}{\mathbb{E}}[z]\\ & =\underset{a}{\arg max}Q(x,a)\end{array}$

这两者便等价了。

在IQN中，我们倾向于使用第二种表示，因为它可以推导出一种很容易计算的表示。

不难证明， ${\int }_0^1{F}_Z^{-1}(\tau )d\beta (\tau )={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}z\frac{\mathrm{\partial }}{\mathrm{\partial }z}(\beta \circ F_Z)(z)dz$

令 $z=F_Z^{-1}(\tau )$

$\begin{array}{rl}{\int }_0^1{F}_Z^{-1}(\tau )d\beta (\tau )& \stackrel{z=F_Z^{-1}(\tau )}{=}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}zd\beta (F_Z(z))\\ & ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}z\frac{\mathrm{\partial }}{\mathrm{\partial }z}(\beta \circ F_Z)(z)dz\end{array}$

其中 $\beta$ 是一个 $[0,1]\to [0,1]$ ，被称为distortion risk measure，我们定义基于 $\beta$ 的distorted expectation

$Q_{\beta }(x,a):=\underset{\tau \sim U([0,1])}{\mathbb{E}}[Z_{\beta (\tau )}(x,a)]$

其中 $Z_{\tau }:=F_Z^{-1}(\tau )$ ，显然

$Q_{\beta }(x,a):=\underset{\tau \sim U([0,1])}{\mathbb{E}}[Z_{\beta (\tau )}(x,a)]={\int }_0^1{F}_Z^{-1}(\tau )d\beta (\tau )$

这就把 $Q_{\beta }(x,a)$ 和前面的风险偏好联系起来了。

最后，策略可以表示为

$\begin{array}{rl}{\pi }_{\beta }(x)& =\underset{a\in \mathcal{A}}{\arg max}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}z\frac{\mathrm{\partial }}{\mathrm{\partial }z}(\beta \circ F_Z)(z)dz\\ & =\underset{a\in \mathcal{A}}{\arg max}{\int }_0^1{F}_Z^{-1}(\tau )d\beta (\tau )\\ & =\underset{a\in \mathcal{A}}{\arg max}\underset{\tau \sim U([0,1])}{\mathbb{E}}[Z_{\beta (\tau )}(x,a)]\\ & =\underset{a\in \mathcal{A}}{\arg max}{Q}_{\beta }(x,a)\end{array}$

接下来再让我们看看不同的 $\beta$ 就起到什么不同的效果。

整理而言，当 $\beta$ 为凸函数时，偏好是risk-averse的，当 $\beta$ 为凹函数时，偏好是risk-seeking的。

有一些现成的函数可以作为 $\beta$

CPW函数

$\mathrm{C}\mathrm{P}\mathrm{W}(\eta ,\tau )=\frac{{\tau }^{\eta }}{{({\tau }^{\eta }+(1-\tau {)}^{\eta })}^{\frac{1}{\eta }}}$

Wang函数（其中 $\mathrm{\Phi }$ 是标准正态分布的CDF函数）

$\mathrm{Wang}(\eta ,\tau )=\mathrm{\Phi }({\mathrm{\Phi }}^{-1}(\tau )+\eta )$

Pow函数

$\mathrm{Pow}(\eta ,\tau )=\{\begin{array}{ll}{\tau }^{\frac{1}{1+|\eta |}},& \text{ if }\eta \ge 0\\ 1-(1-\tau {)}^{\frac{1}{1+|\eta |}},& \text{ otherwise }\end{array}$

conditional value-at-risk函数

$\mathrm{C}\mathrm{V}\mathrm{a}\mathrm{R}(\eta ,\tau )=\eta \tau$

这些函数的 $\eta$ 都可以看作是超参数，而 $\tau$ 则是自变量，例如

$\beta (\tau )=\text{Wang}(.75,\tau )$

下面是有关这些函数的图像

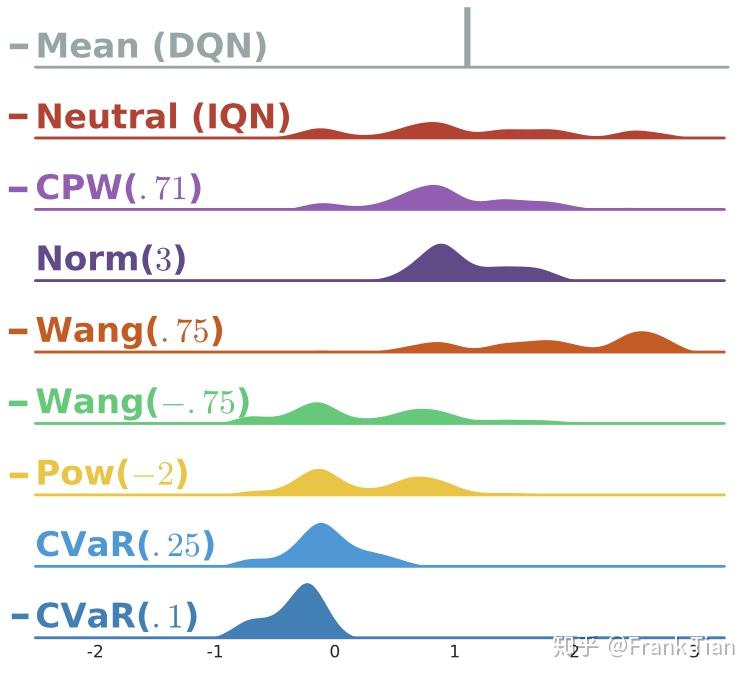
第二列的Neutral是原始的 $Z(s,a)$ 的分布，而其他列的图像都是经过加工后的 $Z_{\beta }(s,a)$ 的图像。

可以看到，这些不同的 $\beta$ 有些对风险比较积极，例如 $\text{Wang}(.75)$ ，而有些则很保守，只集中在原分布中值比较大的部分，例如 $\text{CPW}(.71)$ 。

最后，让我们步入正题，看看IQN是怎么训练的。

下面的图很好的描绘来DQN，C51，QR-DQN和IQN的区别。

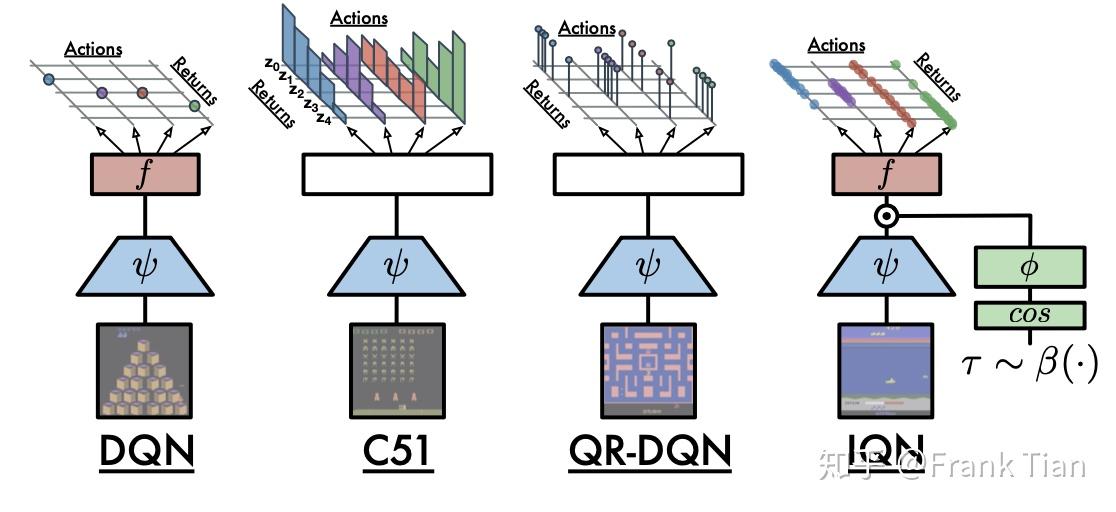
C51，QR-DQN和IQN都是想去学习一个分布，但是它们的方式并不一样。

C51和QR-DQN是去找到了一种间接的方式去表示这个分布，也就是用atoms的方式。

而IQN更像是直接的学出了这个分布。

IQN的输入和输出是什么呢？

它是输入是状态 $s$ ，和采样$\tau \sim U[0,1]$ ，而输出和DQN很像，是一个 $|\mathcal{A}|$ 维的向量。

区别在于，DQN只能输出每个动作的期望，而IQN可以根据输入的 $\tau$ ，输出每个动作的 $\tau$ 分位数。

这样看来，IQN和C51，QR-DQN的不同之处在于，它不在想办法表示这个分布，它直接就是这个分布！

那这个前面提到的Risk-Sensitive强化学习有什么关系呢？

试想，如果我们可以学习出 $Z_{\tau }(x,a)$ ，那么不就可以计算出对于任何 $\beta$ 的 $Q_{\beta }(x,a)$ 了吗？这样我们就可以在作出决定的时候根据我们的偏好，而不是只能根据期望 $Q(x,a)$ 去计算。

那么，最后的问题，这个网络怎么训练呢？

首先还是从Buffer中拿到采样 $(s,a,r,s^{\mathrm{\prime }})$ 。

接下来我们要根据 $s^{\mathrm{\prime }}$ 选出最好的动作 $a^{\ast }$ 。

但是，这里我们不再用 $Z(x,a)$ 算出 $Q(x,a)$ 选择了，而是应该加入偏好 $\beta$ ，当然，如果没有特殊的偏好，令 $\beta (x)=x$ 即可。

我们需要事先设定一个超参数 $K$ ，用来决定计算 $Q_{\beta }(x,a)$ 的采样次数，于是

$Q_{\beta }(x^{\mathrm{\prime }},a^{\mathrm{\prime }})=\frac{1}{K}\sum _k^K{Z}_{{\tilde{\tau }}_k}(x^{\mathrm{\prime }},a^{\mathrm{\prime }})$

其中

${\tilde{\tau }}_k\sim \beta (\cdot )$

于是

$a^{\ast }\leftarrow \arg \underset{a^{\mathrm{\prime }}}{max}\frac{1}{K}\sum _k^K{Z}_{{\tilde{\tau }}_k}(x^{\mathrm{\prime }},a^{\mathrm{\prime }}),{\tilde{\tau }}_k\sim \beta (\cdot )$

接下来我们要缩短 $Z(x,a)$ 和 $r+\gamma Z(x^{\mathrm{\prime }},a^{\ast })$ 这两个分布之间的距离。

但是我们现在没有某种表示去表示这个分布了，我们的网络就是分布本身。

因此我们需要从网络中采样，来估计这两个分布。我们又引入两个超参数 $N,N^{\mathrm{\prime }}$ ，分别代表估计这两个分布所需要的采样次数，于是有

${\tau }_i,{\tau }_j^{\mathrm{\prime }}\sim U([0,1]),1\le i\le N,1\le j\le N^{\mathrm{\prime }}$

对于两个单独的 ${\tau }_i,{\tau }_j^{\mathrm{\prime }}$ ，它们之间的差表示为

${\delta }_t^{{\tau }_i,{\tau }_j^{\mathrm{\prime }}}=r_t+\gamma Z_{{\tau }_j^{\mathrm{\prime }}}(x_{t+1},{\pi }_{\beta }\left(x_{t+1}\right))-Z_{{\tau }_i}(x_t,a_t)$

那么总的差值就是

$\mathcal{L}(x_t,a_t,r_t,x_{t+1})=\frac{1}{N^{\mathrm{\prime }}}\sum _{i=1}^N\sum _{j=1}^{N^{\mathrm{\prime }}}{\rho }_{{\tau }_i}^{\kappa }\left({\delta }_t^{{\tau }_i,{\tau }_j^{\mathrm{\prime }}}\right)$

我们没有用 ${\left({\delta }_t^{{\tau }_i,{\tau }_j^{\mathrm{\prime }}}\right)}^2$ 而是用 $|{\delta }_t^{{\tau }_i,{\tau }_j^{\mathrm{\prime }}}|$ 这是因为我们本质上还是在做分位数回归，而不是标准的回归。

最后， ${\rho }_{{\tau }_i}^{\kappa }$ 表示的是绝对值函数的软化，我们在上一篇文章中提到过

${\rho }_{\tau }^{\kappa }(u)={\mathcal{L}}_{\kappa }(u)|\tau -{\delta }_{u<0}|$

最终的算法如下