【DRL-6】Distributional DQN: C51

论文

这篇文章开创了一个新的方向，将我们的认知从“Q值”拓展到了“Q分布”。

提要：Distributional DQN算是对DQN的扩展，是model-free，off-policy，value-based，discrete的方法。

其实深究的话这应该叫做"distribution-based"，只不过似乎没有人这么叫。

听说点赞的人逢投必中。

注：这篇文章中的 $x$ 和 $s$ 都表示“状态”的含义。

建议先读

Frank Tian：用Bellman算子理解动态规划150 赞同 · 15 评论文章

这篇文章的数学推导很复杂，我先来介绍一些基本概念。

Bellman算子

首先是算子operator，可以粗浅的理解为

• 函数的输入是集合，输出是集合
• 泛函的输入是函数，输出是集合
• 算子的输入是函数，输出是函数

举个例子，我们知道 $Q(s,a)$ 是一个函数，如果 $s$ 是一个 $n$ 维的向量， $a$ 是一个 $m$ 维的向量，那么 $Q$ 是一个 ${\mathbb{R}}^n\times {\mathbb{R}}^m\to \mathbb{R}$ 的函数，写作

$Q:{\mathbb{R}}^n\times {\mathbb{R}}^m\to \mathbb{R}$

那么，我们可以引入Bellman operator，Bellman operator是针对于某一个具体的策略 $\pi$ 的，对于某一个具体的策略 $\pi$ ，我们有

${\mathcal{T}}^{\pi }Q(x,a):=\mathbb{E}R(x,a)+\gamma \underset{P,\pi }{\mathbb{E}}Q(x^{\mathrm{\prime }},a^{\mathrm{\prime }})$

在上面的例子中，有两个函数，分别是

$Q:{\mathbb{R}}^n\times {\mathbb{R}}^m\to \mathbb{R}$

$R:{\mathbb{R}}^n\times {\mathbb{R}}^m\to \mathbb{R}$

而函数 $R$ 是环境的一部分，我们先不考虑它， $\gamma$ 则先省略，那么算子 ${\mathcal{T}}^{\pi }$ 作用于函数 $Q$ ，也就是输入了一个函数，应该输出一个新的函数，可以写作

${\mathcal{T}}^{\pi }(Q)=Q^{\mathrm{\prime }}$

而这里的 $Q^{\mathrm{\prime }}$ 就是 $\mathbb{E}R(x,a)+\gamma \underset{P,\pi }{\mathbb{E}}Q(x^{\mathrm{\prime }},a^{\mathrm{\prime }})$ ，显然，这也是一个 ${\mathbb{R}}^n\times {\mathbb{R}}^m\to \mathbb{R}$ 的函数。

所以上面的式子应该其实写作

$({\mathcal{T}}^{\pi }(Q))(x,a):=\mathbb{E}R(x,a)+\gamma \underset{P,\pi }{\mathbb{E}}Q(x^{\mathrm{\prime }},a^{\mathrm{\prime }})$

这表示 $Q$ 是一个函数，它作为 ${\mathcal{T}}^{\pi }()$ 这个算子的输入，而输出 ${\mathcal{T}}^{\pi }(Q)$ 也是一个函数，它作为一个整体表示成 $({\mathcal{T}}^{\pi }(Q))$ ，是一个 ${\mathbb{R}}^n\times {\mathbb{R}}^m\to \mathbb{R}$ 的函数，接受变量 $(x,a)$ 。

也可以简写作

$({\mathcal{T}}^{\pi }Q)(x,a):=\mathbb{E}R(x,a)+\gamma \underset{P,\pi }{\mathbb{E}}Q(x^{\mathrm{\prime }},a^{\mathrm{\prime }})$

不管怎么样习惯就好。

那么，我们做策略评估，其实就是在找一个函数 $Q$ ，满足 ${\mathcal{T}}^{\pi }Q=Q$ ，也就是在找算子 ${\mathcal{T}}^{\pi }$ 的不动点。当然因为 ${\mathcal{T}}^{\pi }$ 是一个算子，它的不动点则是一个函数，可以表现为tabular这种离散的映射，也可以是一个神经网络。

接下来我们还可以定义optimality operator，它和bellman operator很像

$\mathcal{T}Q(x,a):=\mathbb{E}R(x,a)+\gamma {\mathbb{E}}_P\underset{a^{\mathrm{\prime }}\in \mathcal{A}}{max}Q(x^{\mathrm{\prime }},a^{\mathrm{\prime }})$

同样的，我们做最优策略的搜索，就是在找算子 $\mathcal{T}$ 的不动点。

接下来，我们可以证明 ${\mathcal{T}}^{\pi }$ 和 $\mathcal{T}$ 都是 $\gamma -\text{ contraction}$ 的，也就是对任意的 $Q_1,Q_2$ 有

$\mathrm{dist}({\mathcal{T}}^{\pi }{Q}_1,{\mathcal{T}}^{\pi }{Q}_2)\le \gamma \mathrm{dist}(Q_1,Q_2)$

$\mathrm{dist}(\mathcal{T}{Q}_1,\mathcal{T}{Q}_2)\le \gamma \mathrm{dist}(Q_1,Q_2)$

这里的 $\text{dist}$ 其实就是无穷范数的意思，用来表示直径。这部分的介绍可以参考我上面的文章。

于是根据Contraction Mapping Theorem， ${\mathcal{T}}^{\pi }$ 和 $\mathcal{T}$ 都有唯一的不动点，我们有

${{\mathcal{T}}^{\pi }}^{\mathrm{\infty }}Q=Q^{\pi }$

${\mathcal{T}}^{\mathrm{\infty }}Q=Q^{\ast }$

KL散度

老生常谈了，对于分布 $p,q$ ，它们的KL散度定义为

$\mathrm{K}\mathrm{L}(p\Vert q)=\int p(x)\log \frac{p(x)}{q(x)}dx$

对于离散的情况，我们还可以展开

$\mathrm{K}\mathrm{L}(p\Vert q)=\sum _{i=1}^{N}p\left(x_i\right)\log \frac{p\left(x_i\right)}{q\left(x_i\right)}=\sum _{i=1}^{N}p\left(x_i\right)[\log p\left(x_i\right)-\log q\left(x_i\right)]$

接下来我们进入正题。

所谓的Distributional DQN，就是把传统DQN中的value function换成了value distribution。

原来的DQN中的值函数是 $Q(s,a)$ ，它是 ${\mathbb{R}}^n\times {\mathbb{R}}^m\to \mathbb{R}$ 的函数，也就和说，它接受一个 $s,a$ ，输出一个实数，这个实数就是这个状态动作对 $a,s$ 的评估。

而Distributional DQN中的值分布，它接受一个 $s,a$ ，输出一个分布，这个分布描绘了状态动作对 $a,s$ 的所有取值的可能性。

简单来说，值函数可以看作值分布的期望。

我们用 $Z(x,a)$ 表示值分布，这个分布应该类似 $P(v|x,a)$ ，也就是说是一个条件分布，当给定 $x,a$ 之后就变成了一个具体的分布。其中 $v$ 是一个一维的实数。

基于值分布的定义，我们再来看看MDP的过程是怎么进行的。

现在针对值分布，我们可以定义转移算子

$\begin{array}{rl}{P}^{\pi }Z(x,a)& :=Z(X^{\mathrm{\prime }},A^{\mathrm{\prime }})\\ X^{\mathrm{\prime }}& \sim P(\cdot |x,a),A^{\mathrm{\prime }}\sim \pi (\cdot |X^{\mathrm{\prime }})\end{array}$

这个算子 $P^{\pi }$ 是 $\mathcal{Z}\to \mathcal{Z}$ ，也就是从一个分布到另一个分布。

那么值分布情况下的Bellman operator就可以定义为

${\mathcal{T}}^{\pi }Z(x,a):\stackrel{D}{=}R(x,a)+\gamma P^{\pi }Z(x,a)$

其实我们的思路是比较清晰的，按照DQN的想法，我们计算出一个 $y=r+\gamma Q(x^{\mathrm{\prime }},a^{\ast })$ ，然后让当前的 $Q(x,a)$ 向这个 $y$ 靠近就可以了。

在DQN的情况中， $y$ 是一个实数， $Q(x,a)$ 也是一个实数。

而到了Distributional DQN中，我们不再使用 $Q(x,a)$ 表示“值”了，我们不再用期望来估计这个值的情况，而是直接使用它的分布， $Q(x,a)$ 和 $Z(x,a)$ 满足

$Q(x,a)=\mathbb{E}[Z(x,a)]$

那么在Distributional DQN中，我们想要的是让 $Z(x,a)$ 这个分布尽可能的靠近某个分布。

我们定义Distributional DQN情况下的optimality operator，即

$\mathcal{T}Z={\mathcal{T}}^{\pi }Z\text{ for some }\pi \in {\mathcal{G}}_Z$

其中

${\mathcal{G}}_Z:=\{\pi :\sum _a\pi (a|x)\mathbb{E}Z(x,a)=\underset{a^{\mathrm{\prime }}\in \mathcal{A}}{max}\mathbb{E}Z(x,a^{\mathrm{\prime }})\}$

于是，在Distributional DQN中，我们要做的是让 $Z(x,a)$ 这个分布尽可能靠近 $(\mathcal{T}Z)(x,a)$ 这个分布。

现在的问题是，我们如何表示这个分布呢？

表示分布当然有很多方法，但是我们很快就抛弃掉了高斯分布这种参数化的方法，因为它是单峰的。

我们使用Distributional DQN就是希望它能实现多个峰值的值分布，从而学习到更好的结果。

这篇论文的作者们提出了一个叫做C51的算法，它用51个等间距的atoms描绘一个分布，如下所示

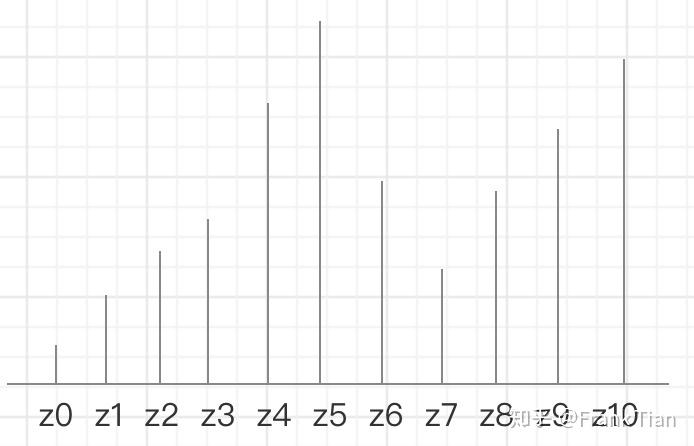
实际上和直方图区别不大，只不过直方图注重的是“区间”，这种被成为comb form的方法注重的是“点”。

当然，这个分布肯定是近似的结果，如何选择点的范围和个数取决于你的应用。

我们现设现在已经训练好了Distributional DQN，那么它的网络架构应该张什么样呢？

还记得在DQN中，网络的输入是 $s$ ，输出是一个向量 $(Q(s,a_1),Q(s,a_2),\cdots ,Q(s,a_m))$

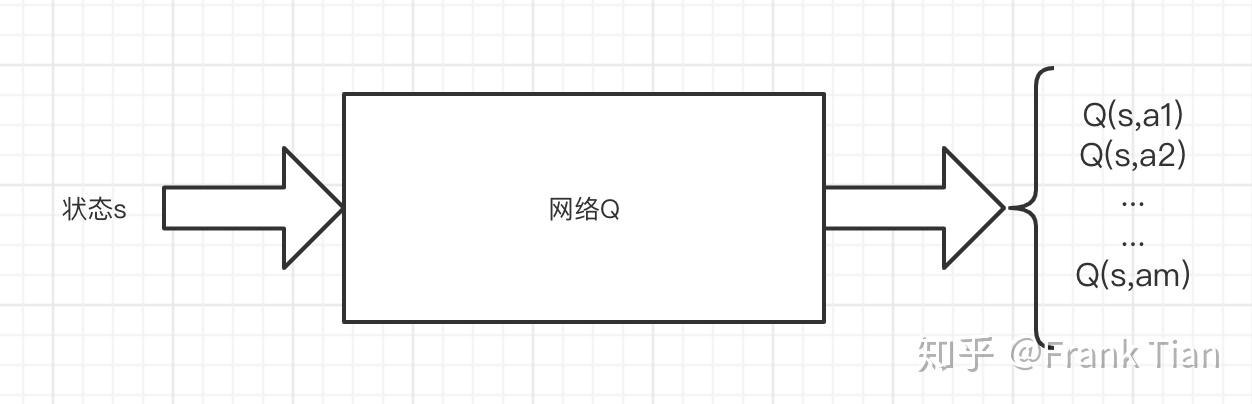
而在Distributional DQN中，输入依旧是一个状态 $s$ ，输出则应该变成了一个矩阵，这个矩阵的每一行代表一个动作 $a$ ，而列数则和你选择的atoms的个数相等，我们设这个数是 $N$ ，那么在C51中， $N=51$ 。

每一列的这 $N$ 个数表示的是什么呢？

我们之前说atoms的位置是你提前人为确定的，比如这个任务中值函数可能的范围是 $(-10,10)$ ，你选择的 $N=11$ ，那么atoms就应该是

$\{-10,-8,-6,-4,-2,0,2,4,6,8,10\}$

我们用 $z$ 表示这个向量，于是atoms可以表示为 $\{z_0,z_1,\cdots ,z_{N-1}\}$ 。

那么这个神经网络输出的矩阵的每一行应该是，针对于某个 $a$ 的一组 $N$ 个概率， $\{p_0^a,p_1^a,\cdots ,p_{N-1}^a\}$ 。

这组 $N$ 个概率 $\{p_0^a,p_1^a,\cdots ,p_{N-1}^a\}$ ，结合atoms的位置 $\{z_0,z_1,\cdots ,z_{N-1}\}$ ，描绘了 $Z(x,a)$ 这个分布。

更一般的，我们有

$Q(x,a)=\mathbb{E}[Z(x,a)]\approx \sum _{i=0}^N{z}_i{p}_i^a$

于是有

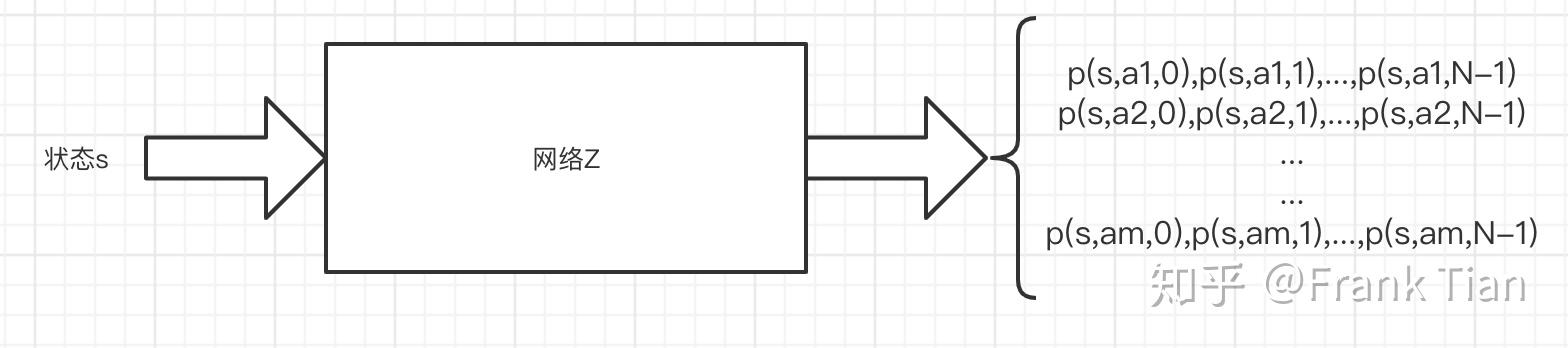
如何让神经网络输出的矩阵保证每行都是一组离散的分布呢？

很简单，只要做一个类似Softmax的操作就可以了。

现在我们的网络已经定义完了，接下来的问题是如何训练。

我们只需要找到损失函数，然后计算它的梯度就可以了。

那么，如何定义损失函数呢？

其实这是一个大问题。这取决于我们如何定义两个分布之间的度量。

使用Wasserstein Metric

$d_p(F,G):=\underset{U,V}{inf}\Vert U-V{\Vert }_p$

可以保证我们的Bellman operator是 $\gamma -\text{ contraction}$ ，也就是可以收敛到唯一的不动点。

但是对于Q-learning用到的optimality operator，并没有这样的理论保证。

更糟糕的是，在实际训练中，SGD是没办法保持这个Wasserstein Metric的。

于是，作者们提出了一个启发式的方法：干脆用KL散度去衡量两个分布的距离。

我们之前介绍过了KL散度离散形式下的计算，非常简单啊。

但是现在还有一个问题，那就是 $r+\gamma Z(s^{\mathrm{\prime }},a^{\ast })$ 并不是“standard comb form“。

我们模拟一遍整个过程就可以发现问题了。

首先，我们从Buffer中采样一个 $(s,a,r,s^{\mathrm{\prime }})$ ，接下来，我们要计算 $y$ ，也就是 $r+\gamma Z(s^{\mathrm{\prime }},a^{\ast })$ 这个分布。

首先， $a^{\ast }$ 从何而来呢？

因为 $Z(s^{\mathrm{\prime }},a)$ 是分布的分布，我们不方便比较同一个 $s$ 下哪一个 $a$ 更好，那干脆从 $Q(s^{\mathrm{\prime }},a)$ 中挑出一个 $a^{\ast }$ ，于是

$\begin{array}{rl}& Q(s_{t+1},a):=\sum _i{z}_i{p}_i(s_{t+1},a)\\ & a^{\ast }\leftarrow \arg \underset{a}{max}Q(s_{t+1},a)\end{array}$

那接下来，我们拿到target network中 $Z(s^{\mathrm{\prime }},a^{\ast })$ 的结果，应该是一组 $N$ 维的向量，表示一个分布，我们设这个向量是 $p^{\mathrm{\prime }}$ 。

那么 $r+\gamma Z(s^{\mathrm{\prime }},a^{\ast })$ 这个分布就可以表示为

• 有 $p_0^{\mathrm{\prime }}$ 的概率取 $r+\gamma z_0$
• 有 $p_1^{\mathrm{\prime }}$ 的概率取 $r+\gamma z_1$
• ...
• 有 $p_{N-1}^{\mathrm{\prime }}$ 的概率取 $r+\gamma z_{N-1}$

但是，我们 $Z(s,a)$ 的输出结果也是一组 $N$ 维的向量，表示一个分布，我们设这个向量是 $p$ ，那么 $Z(s,a)$ 表示为

• 有 $p_0$ 的概率取 $z_0$
• 有 $p_1$ 的概率取 $z_1$
• ...
• 有 $p_{N-1}$ 的概率取 $z_{N-1}$

它们，没有，对齐！

比如这样的

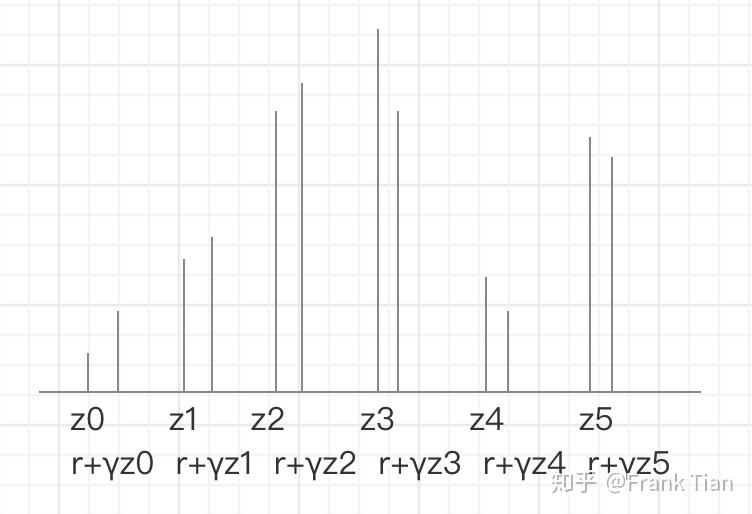
但是atoms的位置是我们一开始就选择好的，自然不能让他随便乱动，所以我们要把它对齐。

用上图的例子，就是把 $r+\gamma z_0$ 分摊到 $z_0$ 和 $z_1$ 上，把 $r+\gamma z_1$ 分摊到 $z_1$ 和 $z_2$ 上，以此类推。

至于如何分摊，按照 $r+\gamma z_0$ 到 $z_0$ 和 $z_1$ 的距离的反比就可以了。

最后，我们在根据atoms相同的两组分布，也就是 $Z(s,a)$ 和经过调整的 $r+\gamma Z(s^{\mathrm{\prime }},a^{\ast })$ 来计算KL散度，算出梯度用来梯度下降。

完整的算法如下

中间那个 $l$ 啊， $m$ 啊，看起来挺复杂，实际上就是在做我说的分摊。而 $m$ 就是 $r+\gamma Z(s^{\mathrm{\prime }},a^{\ast })$ 经过调整的结果。