强化学习——每次访问MC方法和首次访问MC方法的相关理论证明

北京地平线信息技术有限公司算法工程师

前言

本文主要给出每次访问MC方法和首次访问MC方法的相关理论证明，方便大家从根本上去理解这两种方法。

示例——首次访问MC方法和每次访问MC方法的区别

首次访问蒙特卡洛策略评估

在给定一个策略，使用一系列完整episode评估某一个状态 $s$ 时，对于每一个episode，仅当该状态 $s$ 首次出现的时间 $t$ 列入计算：

状态出现的次数加1： $N(s) \leftarrow N(s) + 1$

总的收获值更新： $S(s) \leftarrow S(s) + G_{t}$

状态 $s$ 的价值： $V(s) = S(s) / N(s)$

当 $N(s) \rightarrow \infty$ 时， $V(s) \rightarrow v_{\pi}(s)$

每次访问蒙特卡洛策略评估

在给定一个策略，使用一系列完整的episode评估某一个状态 $s$ 时，对于每一个episode，状态 $s$ 每次出现在状态转移链时，例如，一次在时刻 $t_1$ ，一次在时刻 $t_2$ ，则两次对应的 $G_{t_1}$ ， $G_{t_2}$ 都要用于计算 $s$ 对应的值。

状态出现的次数加1： $N(s) \leftarrow N(s) + 1$

总的收获值更新： $S(s) \leftarrow S(s) + G_{t}$

状态s的价值： $V(s) = S(s) / N(s)$

当 $N(s) \rightarrow \infty$ 时， $V(s) \rightarrow v_{\pi}(s)$

详情请参考：

搬砖的旺财：David Silver 增强学习——Lecture 4 不基于模型的预测zhuanlan.zhihu.com

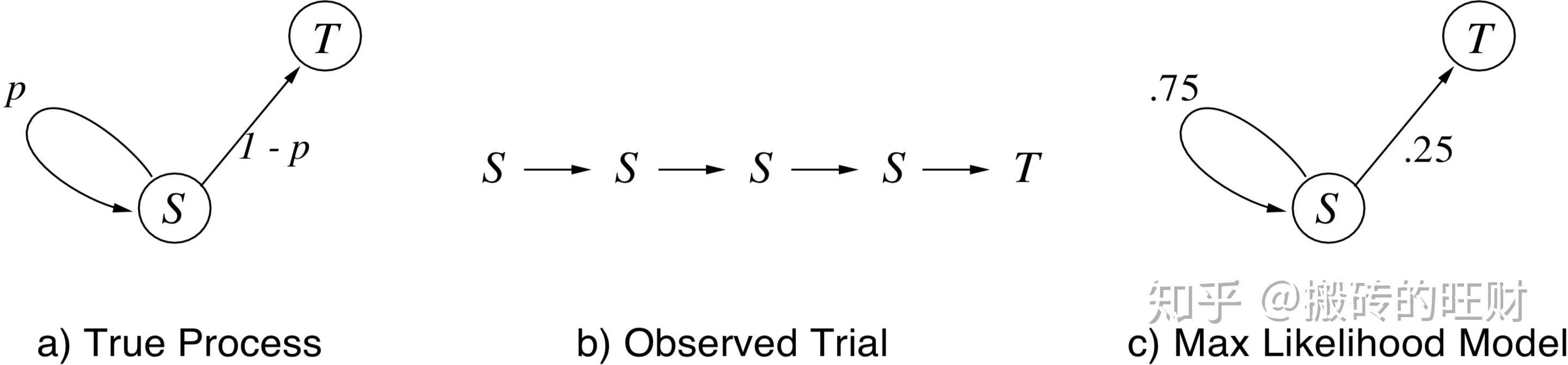
首先考虑图1 a)中所示的马尔可夫链，在每一步中，链或者以概率 $p$ 保持在 $S$ 中，或者以概率 $1-p$ 前往 $T$ 结束。假设我们想要估计从状态 $S$ 开始到终止前的预期步数。考虑从估计值函数入手，那么假设每一步都会得到 $+1$ 的奖励，在这种情况下 $V\left( S \right)$ 等于终止前的预期步数。假设已经观察到的唯一数据是由马尔可夫链产生的单个试验——该试验持续4个步骤， $3$ 个从 $S$ 传递到 $S$ ，并且 $1$ 个从 $S$ 传递到 $T$ ，如图2 b)所示。那么两个MC方法从这个试验中将会得出什么结论？

我们假设这些方法不知道马尔可夫链的结构。它们所知道的只是图1 b)中所示的试验。

首次访问MC方法（first-visit MC）实际上观察到的是从第一次访问 $S$ 到 $T$ 的单次遍历（singel traversal）。该遍历持续 $4$ 步，因此其对 $V\left( S \right)$ 的估计为 $4$ 。

另一方面，每次访问MC方法（every-visit MC）实际上观察到的是从 $S$ 到 $T$ 的 $4$ 个单独的遍历，一个有 $4$ 个步骤，一个有 $3$ 个步骤，一个有 $2$ 个步骤，一个有 $1$ 个步骤。对这四个有效试验进行平均，每次访问MC方法估计的 $V\left( S \right)$ 为 $\frac{1+2+3+4}{4}=2.5$ 。

哪个估计值更好呢？ $4$ 还是 $2.5$ 呢？我们将在下面说明，实际上 $4$ 是无偏的答案， $2.5$ 在统计意义上存在偏差。

接下来计算上例的ML估计。如果马尔可夫链的最大似然模型（如图1 c)所示）完全正确，那么在终止之前期望的时间步数是多少呢？对于每个可能的步数转移概率的最大似然估计（Maximum-Likelihood estimate，ML estimate）是 $\frac{3}{4}$ ， $\textrm{S-to-T}$ 转移概率的最大似然估计是 $\frac{1}{4}$ 。没有观察到其他状态的转移，因此估计它们的概率为 $0$ 。那么马尔可夫链的最大似然模型如图1 c)所示。

如果马尔可夫过程的最大似然模型完全正确，我们即认为值函数的ML估计是完全正确的。

接下来计算上例的ML估计。如果马尔可夫链的最大似然模型完全正确，那么在终止之前期望的时间步数是多少呢？对于每个可能的步数 $k$ ，我们可以计算其发生的概率，然后计算期望：

$\begin{align*} V^{\textrm{ML}}\left( S \right) &=\sum_{k=1}^{\infty}{\textrm{Pr}}\left( k \right)k\\ &=\sum_{k=1}^{\infty}\left( 0.75 \right)^{k-1}\cdot\left( 0.25 \right)\cdot k \\ &=4 \end{align*}$

因此，在该例中，ML估计与首次访问MC方法的估计相同。

定理1 For any undiscounted absorbing Markov chain, the estimates computed by first-visit MC are the reduced-ML estimates, for all states and after all trials.

简化的双状态抽象马尔可夫链

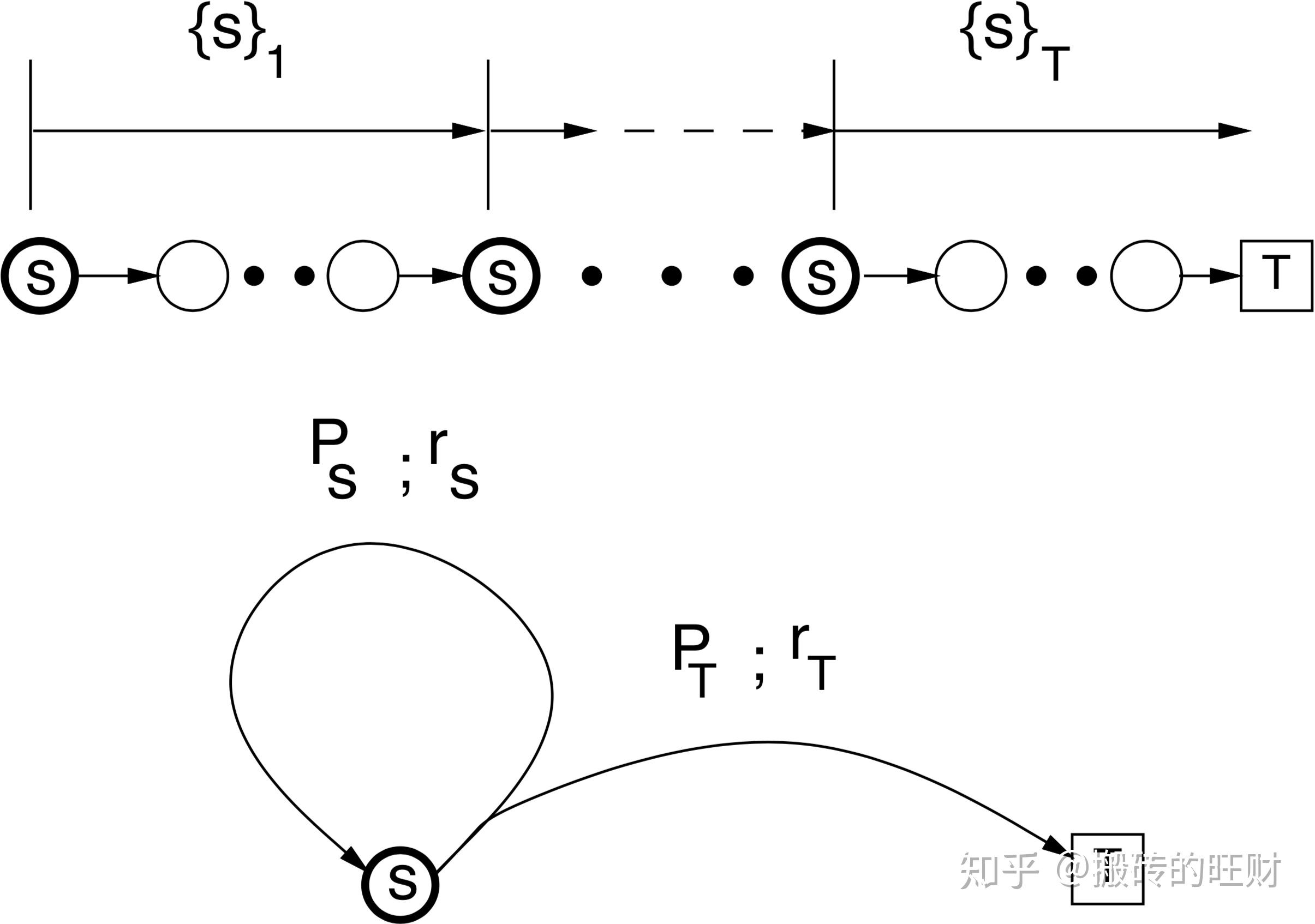
在本文中，我们将介绍如何将任意的undiscounted absorbing Markov chain简化为双状态抽象马尔可夫链（two-state abstracted Markov chain），并将它用在MC方法中。简化的依据是独立关注每个状态。假设我们只对一个状态 $s$ 的价值感兴趣，并且所有的试验都是从状态 $s$ 开始。我们可以在不失一般性的情况下做到这一点，因为状态 $s$ 的价值在试验后的变化不受首次访问该状态之前发生的任何事情的影响。

对于任意的马尔可夫链，试验产生两个序列，一个随机的状态序列， $\left\{ s \right\}$ ，以 $s$ 开头并以 $T$ 结尾，以及相关的随机奖励序列 $\left\{ r \right\}$ 。将序列 $\left\{ s \right\}$ 分成连续的子序列，这些子序列以 $s$ 开头并在下一次重新访问 $s$ 之前结束。第 $i$ 次重新访问 $s$ 开始的子序列表示为 $\left\{ s \right\}_i$ 。最后一个这样的子序列是特殊的，因为它以终止状态结束并表示为 $\left\{ s \right\}_T$ 。相应的奖励序列类似地表示为 $\left\{ r \right\}_i$ 和 $\left\{ r \right\}_T$ 。由于马尔可夫性，对于所有的 $i\ne j$ ， $\left\{ s \right\}_i$ 独立于 $\left\{ s \right\}_j$ ，类似地 $\left\{ r \right\}_i$ 独立于 $\left\{ r \right\}_j$ 。这是很有意义的，意味着在访问状态 $s$ 之间实际发生的精确状态序列在首次访问MC方法（或者每次访问MC方法）估计 $V\left( s \right)$ 时不起作用。同样，精确的奖励顺序 $\left\{ r \right\}_i$ 也无关紧要，因为在MC方法中只使用了访问状态 $s$ 之间的奖励总和。

因此，为了便于分析，可以将任意的undiscounted Markov chain简化为图2下面部分所示的双状态抽象链。

图2 抽象的马尔可夫链。图中上面部分是典型的状态序列。对于访问状态s而言，序列可以被分成连续的子序列。为了便于分析，在重新访问s之间的状态和奖励的精确顺序无关紧要。因此，在考虑s的值时，可以将任意的undiscounted Markov chains抽象为图中下面部分所示的双状态链（two-state chain）

首次访问MC方法 first-visit MC

设 $\left\{ x \right\}$ 代表成对的随机序列 $\left( \left\{ s \right\},\left\{ r \right\} \right)$ 。

首次访问MC方法通过 $1$ 次试验后得到的序列 $\left\{ x \right\}$ 估计的 $V\left( s \right)$ 是 ${V_1^F}\left( s \right)=f\left( \left\{ x \right\} \right)=r_{s_1}+r_{s_2}+r_{s_3}+...+r_{s_k}+r_{T}$ 。

其中 $k$ 是随机数，代表第 $k$ 次重新访问状态 $s$ ， $r_{s_i}$ 是序列 $\left\{ r \right\}_i$ 中各个奖励的总和， $r_T$ 是最后一次访问状态 $s$ 后收到的总的随机奖励。

对于所有的 $i$ ， $E\left\{ r_{s_i} \right\}= R_s$ 。

首次访问MC方法通过 $n$ 次试验后得到的序列 $\left\{ x \right\}^1,\left\{ x \right\}^2,...,\left\{ x \right\}^n$ 估计的 $V\left( s \right)$ 是 ${V_n^F}\left( s \right)=f\left( \left\{ x \right\}^1, \left\{ x \right\}^2,... \left\{ x \right\}^n\right)=\frac{\sum_{i=1}^{n}f\left( \left\{ x \right\}^i\right)}{n}$ 。

从字面上的意思来理解， $V_n^F(s)$ 只是来自 $n$ 个样本 $\left\{ x \right\}^1, \left\{ x \right\}^2,...,\left\{ x \right\}^n$ 估计的平均值，由于马尔可夫性，样本是独立的。

每次访问MC方法 every-visit MC

每次访问MC方法通过 $1$ 次试验得到的序列 $\left\{ x \right\}$ 估计的 $V\left( s \right)$ 值为 $V_1^E\left( s \right)=t\left( \left\{ x \right\} \right)=\frac{t_{num}\left( \left\{ x \right\} \right)}{k+1}=\frac{r_{s_1}+2r_{s_2}+...+kr_{s_k}+\left( k+1 \right)r_T}{k+1}$ 。

其中 $k$ 是随机数，代表第 $k$ 次重新访问状态 $s$ 。每次重新访问 $s$ 都有效地开始了另一次试验（如图1所示）。因此，在第 $i$ 次和第 $i+1$ 次访问状态 $s$ 之间发生的奖励在估计时被包括了 $i$ 次。每次访问MC通过 $n$ 次试验后得到的序列 $\left\{ x \right\}^1,\left\{ x \right\}^2,...,\left\{ x \right\}^n$ 估计的 $V\left( s \right)$ 是 $V_n^E\left( s \right)=t\left( \left\{ x \right\}^1,\left\{ x \right\}^2,...,\left\{ x \right\}^n \right)=\frac{{\sum_{i=1}^n}t_{num}\left( \left\{ x \right\}^i \right)}{{\sum_{i=1}^n}\left( k_i+1 \right)}$ 。

其中 $k_i$ 是第 $i$ 次试验 $\left\{ x \right\}^i$ 中状态 $s$ 的重访次数。与首次访问MC方法的估计器不同， $n$ 次试验的每次访问MC方法的估计器不仅仅是单个试验估计值的平均，这使得它的分析更加复杂。

我们可以得出首次访问MC方法和每次访问MC方法的偏差（Bias）和方差（Var）——它们是试验次数 $n$ 的函数。均方误差（Mean Squared Error，MSE）是 ${\textrm{Bias}}^2+\textrm{Var}$ 。

相关概念说明

$r_s$ 和 $r_T$ 分别表示与图2中 $s\rightarrow s$ 与 $s\rightarrow T$ 转移有关的随机奖励。

$S_s$ 表示从 $s$ 到 $s$ （包括最开始的状态 $s$ ）可能发生的所有状态序列的集合， $S_T$ 表示从 $s$ 到 $T$ （包括状态 $s$ ）可能发生的所有状态序列的集合。

$P_T$ 和 $P_s$ 分别表示在抽象链中终止和循环的概率。

其中 $P_T=\sum_{ {\left\{ s \right\}_T}\in S_T}P\left( {\left\{ s \right\}_T} \right)$ 。

定义 $P_s = 1-P_T$ 。

奖励概率定义如下：

$Prob\left\{ r_s=q \right\}=\prod_{\left\{ s \right\}\in S_s}P\left( \left\{ s \right\} \right)P\left( r_\left\{ s \right\}=q|\left\{ s \right\} \right)$

$Prob\left\{ r_T=q \right\}=\prod_{\left\{ s \right\}_T\in S_T}P\left( \left\{ s \right\}_T \right)P\left( r_T=q|\left\{ s \right\}_T \right)$

因此：

$R_s = E\left\{ r_s \right\}=\sum_qq\ Prob\left\{ r_s=q \right\}$

$R_T=E\left\{ r_T \right\}=\sum_q q\ Prob\left\{ r_T=q \right\}$

同理，

${\textrm{Var}} \left( r_s \right) = E\left\{ \left( r_s- R_s \right)^2 \right\}=\sum_qProb\left\{ r_s=q \right\}\left( q-R_s \right)^2$

${\textrm{Var}} \left( r_T \right) = E\left\{ \left( r_T- R_T \right)^2 \right\}=\sum_qProb\left\{ r_T=q \right\}\left( q-R_T \right)^2$

如果原始的马尔可夫链中奖励是状态转移的确定性函数，那么存在与每个 $\left\{ s \right\}_i$ 相关的单个 $r_i$ 。但是，如果原始的马尔可夫链中奖励是随机的，那么存在与每个 $\left\{ s \right\}_i$ 相关的一组可能的随机 $r_i$ 。还值得注意的是，即使原始的马尔可夫链中的所有个体的奖励都是确定性的， ${\textrm{Var}} \left( r_s \right)$ 和 ${\textrm{Var}} \left( r_T \right)$ 仍然可以大于零，因为 $r_s$ 和 $r_T$ 将是随机的——从 $s$ 到 $s$ 和从 $s$ 到 $T$ 存在许多不同的路径。

注意：

$\begin{align*} E\left[ f\left( \left\{ x \right\} \right) \right]&=\sum_\left\{ x \right\}P\left( \left\{ x \right\} \right)f\left( \left\{ x \right\} \right)\\ &=\sum_kP\left( k \right)E_\left\{ r \right\}\left\{ f\left( \left\{ x \right\} \right)|k \right\} \end{align*}$ （1）

其中 $k$ 是状态 $s$ 的重访次数。如果 $r<1$ ，那么

$\sum_{i=0}^\infty ir^i=\frac{r}{\left( 1-r \right)^2}$

$\sum_{i=0}^\infty i^2r^i=\frac{r\left( 1+r \right)}{\left( 1-r \right)^3}$

定理2 状态 $s$ 的值函数（value function）真值是 $V\left( s \right)=R_T+\frac{P_s}{P_T}R_s$

证明：

图2中状态 $s$ 的值可以从Bellman方程推导出：

$\begin{align*} &V\left( s \right)=P_s\left( R_s+V\left( s \right) \right)+P_T\left( R_T+V_T \right)\\ \Rightarrow&V\left( s \right)=P_sR_s+P_sV\left( s \right)+P_TR_T+P_TV_T \\ \underline{V_T=0} \Rightarrow &\left( 1-P_s \right)V\left( s \right)=P_sR_s+P_TR_T \end{align*}$

因此，

$V\left( s \right)=\frac{P_sR_s+P_TR_T}{1-P_s}=\frac{P_sR_s}{1-P_s}+\frac{P_TR_T}{1-P_s}=\frac{P_sR_s}{P_T}+\frac{P_TR_T}{P_T}=\frac{P_s}{P_T}R_s+R_T$

定理3 首次访问MC方法是无偏的，即 ${\textrm{Bias}}_n^F\left( s \right)=V\left( s \right)-E\left\{ V_n^F\left( s \right) \right\}=0$

因为从开始状态 $s$ 到终止状态 $T$ 的样本路径上的总奖励根据定义是对所有这些路径的期望总奖励的无偏估计。因此，来自 $n$ 个独立样本路径的估计平均值也是无偏的。

证明：

对于单次试验而言，首次访问MC方法是无偏的，由（1）得：

$\begin{align*} E\left\{ V_1^F\left( s \right) \right\} &=E_\left\{ x \right\}\left[ f\left( \left\{ x \right\} \right) \right]\\ &=\sum_kP\left( k \right)E_\left\{ r \right\}\left\{ f\left( \left\{ x \right\} \right)|k \right\}\\ &=\sum_kP_TP_s^k\left( kR_s+R_T \right)\\ &=P_T\sum_k\left( kP_s^k+P_s^kR_T \right)\\ &=P_T\left[ R_s\sum_k\left( kP_s^k \right)+R_T\sum_k\left( P_s^k \right) \right]\\ &\sum_{i=0}^\infty ir^i=\frac{r}{\left( 1-r \right)^2}\Rightarrow \sum_{k=0}^\infty kP_s^k=\frac{P_s}{\left( 1-P_s \right)^2}\\ &\sum_{k=0}^{\infty}r^i=\frac{1}{1-r}\Rightarrow \sum_{k=0}^{\infty}{P_s}^i=\frac{1}{1-P_s}\\ &=P_T\left[ \frac{P_s}{\left( 1-P_s \right)^2}R_s+\frac{1}{1-P_s}R_T \right]\\ &=\frac{P_s}{P_T}R_s+R_T\\ &=V\left( s \right) \end{align*}$

因为 $n$ 次试验后的估计值 $V_n^F\left( s \right)$ 是 $n$ 个独立估计样本的平均值，每个估计值都是无偏的，所以 $n$ 次试验估计也是无偏的。

定理4 每次访问MC方法是有偏的， $n$ 次试验后， ${\textrm{Bias}}_n^E\left( s \right)=V\left( s \right)-E\left\{ V_n^E\left( s \right) \right\}=\frac{2}{n+1}{\textrm{Bias}}_1^E\left( s \right)=\frac{2}{n+1}\left[ \frac{P_s}{2P_T}R_s \right]$ （ $n\rightarrow \infty$ 时每次访问MC方法变为无偏的）

证明：

对于单次试验而言，每次访问MC方法的偏差是：

$\begin{align*} E\left\{ V_1^E\left( s \right) \right\} &=E_\left\{ x \right\}\left[ t\left( \left\{ x \right\} \right) \right]\\ &=\sum_kP\left( k \right)E_\left\{ r \right\}\left\{ t\left( \left\{ x \right\} \right)|k \right\}\\ &=\sum_kP_TP_s^k\left( \frac{R_s+2R_s+...+kR_s+\left( k+1 \right)R_T}{k+1} \right)\\ &=\sum_kP_TP_s^k\left( \frac{k}{2}R_s+R_T \right)\\ &=P_T\left( \frac{1}{2}R_s\sum_k\left( kP_s^k \right)+R_T\sum_{k}\left( P_s^k \right) \right)\\ &\sum_{i=0}^\infty ir^i=\frac{r}{\left( 1-r \right)^2}\Rightarrow \sum_{k=0}^\infty kP_s^k=\frac{P_s}{\left( 1-P_s \right)^2}\\ &\sum_{k=0}^{\infty}r^i=\frac{1}{1-r}\Rightarrow \sum_{k=0}^{\infty}{P_s}^i=\frac{1}{1-P_s}\\ &=P_T\left( \frac{1}{2}R_s\frac{P_s}{\left( 1-P_s \right)^2}+R_T\frac{1}{1-P_s} \right)\\ &=P_T\left( \frac{1}{2}R_s\frac{P_s}{P_T^2}+R_T\frac{1}{P_T} \right)\\ &=\frac{P_s}{2P_T}R_s+R_T \end{align*}$

那么， ${\textrm{Bias}}_1^E\left( s \right)=V\left( s \right)-E\left\{ V_1^E\left( s \right) \right\}=R_T+\frac{P_s}{P_T}R_s-\left( \frac{P_s}{2P_T}R_s+R_T \right)=\frac{P_s}{2P_T}R_s$ 。

在 $n$ 次试验后计算偏差有点复杂，需要用组合数学 $B\left( n;k \right)$ 的形式表示 $k$ 。我们可以把 $B\left( n;k \right)$ 看作是将 $k$ 分解成 $n$ 个非负整数的不同方式的个数——其次序被认为是重要的。因此得到， $B\left( n;k \right)= \begin{pmatrix} k+n-1 \\ n-1 \end{pmatrix}$ 。进一步假设 $B\left( n;k_1,k_2,...,k_n|k \right)$ 是可以获得从 $k_1$ 到 $k_n$ 的不同方式的数量——可以忽略顺序。注意， $\sum_{\textrm{factors of }k}B\left( n;k_1,k_2,...,k_n|k \right)=B\left( n;k \right)$ 。我们使用上标来区分来自不同试验的奖励，例如， $r_j^2$ 指的是在第2次试验中第 $j$ 次和 $j+1$ 次访问 $s$ 之间收到的总的随机奖励。

$\begin{align*} E\left\{ V_n^E\left( s \right) \right\} &=E_\left\{ x \right\}\left\{ \frac{\sum_{i=1}^nt_{num}\left( \left\{ x \right\}^i \right)}{\sum_{i=1}^n\left( k_i+1 \right)} \right\}\\ &=\sum_{k_1,k_2,...,k_n}P\left( k_1,k_2,...,k_n \right)E_\left\{ r \right\}\left\{ \frac{\sum_{i=1}^n\sum_{j=1}^{k_i}jr_{s_j}^i}{\sum_{i=1}^n\left( k_i+1 \right)}|k_1,k_2,...,k_n \right\}\\ &=\sum_kP\left( k \right)\sum_{\textrm{factors of }k}B\left( n;k_1,k_2,...,k_n|k \right)\left[ \frac{\sum_{i=1}^nk_i\left( k_i+1 \right)}{2\left( k+n \right)}R_s+R_T \right]\\ &=R_T+R_s\left( \sum_kP_T^nP_s^k\sum_{\textrm{factors of }k}B\left( n;k_1,k_2,...,k_n|k \right)\left[ \frac{\sum_{i=1}^n\left( k_i \right)^2+k}{2\left( k+n \right)} \right] \right) \end{align*}$

又，

$\sum_{\textrm{factors of }k}B\left( n;k_1,k_2,...,k_n|k \right)\left[ \frac{\sum_{i=1}^n\left( k_i \right)^2+k}{2\left( k+n \right)} \right]=\frac{k}{n+1}B\left( n;k \right)$ （2）

以及，

$\sum_{k=0}^\infty P_s^kP_T^nB\left( n;k \right)\frac{k}{n}=\frac{P_s}{P_T}$

所以得到，

$E\left\{ V_n^E\left( s \right) \right\}=R_T+\frac{n}{n+1}\frac{P_s}{P_T}R_s$

因此 ${\textrm{Bias}}_n^E\left( s \right)=V\left( s \right)-E\left\{ V_n^E\left( s \right) \right\}=\frac{1}{n+1}\frac{P_s}{P_T}R_s$ 。这也证明了每次访问MC方法在 $n\rightarrow\infty$ 时是无偏的。

给出（2）的证明：

将 $T\left( n;k \right)$ 定义为 $k$ 平方因子的所有因子分解的总和：

$T\left( n;k \right)=\sum_{\textrm{factors of }k}B\left( n;k_1,k_2,...,k_n|k \right)\sum_{i=1}^n\left( k_i \right)^2$

存在以下事实：

fact 1： $\sum_{j=0}^kB\left( n;k-j \right)=B\left( n+1;k \right)$

fact 2： $\sum_{j=0}^kjB\left( n;k-j \right)=\frac{kB\left( n+1;k \right)}{n+1}$

fact 3： $\sum_{j=0}^kj^2B\left( n;k-j \right)=\frac{T\left( n+1;k \right)}{n+1}$

fact 4： $T\left( n+1;k \right)=\sum_{j=0}^kT\left( n;k-j \right)+j^2B\left( n;k-j \right)$

fact 3和fact 4暗示着， $T\left( n+1;k \right)=\frac{n+1}{n}\sum_{j=0}^kT\left( n;k-j \right)$

证明一下：
$\begin{align*} T\left( n+1;k \right) &=\sum_{j=0}^kT\left( n;k-j \right)+j^2B\left( n;k-j \right)\\ &=\sum_{j=0}^kT\left( n;k-j \right)+\sum_{j=0}^kj^2B\left( n;k-j \right)\\ &=\sum_{j=0}^kT\left( n;k-j \right)+\frac{T\left( n+1;k \right)}{n+1}\\ &\Rightarrow\\ &\left( 1-\frac{1}{n+1} \right)T\left( n+1;k \right)=\sum_{j=0}^kT\left( n;k-j \right)\\ &\Rightarrow\\ &T\left( n+1;k \right)=\frac{n+1}{n}\sum_{j=0}^kT\left( n;k-j \right) \end{align*}$

使用fact 1、fact 2、fact 3，我们可以证明 $T\left( n;k \right)$ 是递归的解，

因此证明了，

$\begin{align*} &\sum_{\textrm{factors of }k}B\left( n;k_1,k_2,...,k_n|k \right)\left[ \sum_{i=1}^n\left( k_i \right)^2 \right]=\frac{k\left( 2k+n-1 \right)}{n+1}B\left( n;k \right)\Rightarrow\\ &\sum_{\textrm{factors of }k}B\left( n;k_1,k_2,...,k_n|k \right)\left[ \frac{\sum_{i=1}^n\left( k_i \right)^2}{2\left( k+n \right)} \right]+\frac{k}{2\left( k+n \right)}B\left( n;k \right)=\frac{k}{n+1}B\left( n;k \right)\Rightarrow\\ &\sum_{\textrm{factors of }k}B\left( n;k_1,k_2,...,k_n|k \right)\left[ \frac{\sum_{i=1}^n\left( k_i \right)^2+k}{2\left( k+n \right)} \right]=\frac{k}{n+1}B\left( n;k \right) \end{align*}$

定理5 首次访问MC方法的方差为 ${\textrm{Var}}_n^F\left( s \right)=\frac{{\textrm{Var}}_1^F\left( s \right)}{n}=\frac{1}{n}\left[ {\textrm{Var}}\left( r_T \right)+\frac{P_s}{P_T}{\textrm{Var}}\left( r_s \right)+\frac{P_s}{P_T^2}R_s^2 \right]$

证明：

我们首先计算一次试验得到的序列 $\left\{ x \right\}$ 的方差，

$\begin{align*} {\textrm{Var}}_1^F\left( s \right) &=E_\left\{ x \right\}\left\{ \left( \left( f\left\{ x \right\} \right)-V\left( s \right) \right)^2 \right\}\\ &=\sum_kP\left( k \right)E_\left\{ r \right\}\left\{ \left( \left( f\left\{ x \right\} \right)-V\left( s \right) \right)^2|k \right\} \\ &=\sum_kP_TP_s^kE_\left\{ r \right\}\left\{ x \right\}\left\{ \left( \left( \sum_{i=1}^kr_{s_i}+r_T \right)-\left( \frac{P_s}{P_T}R_s+R_T \right) \right)^2|k \right\}\\ &=\sum_kP_TP_s^kE_\left\{ r \right\}\left\{ \sum_{i=1}^k\left( r_{s_i}^2+2r_Tr_{s_i} \right)+2\sum_{i \ne j}r_{s_i}r_{s_j}+r^2_T+\frac{P_s^2}{P_T^2}R_s^2+2\frac{P_s}{P_T}R_sR_T\\+R_T^2-\sum_{i=1}^k2r_{s_i}\left( \frac{P_s}{P_T}R_s+R_T \right)-2r_T\left( \frac{P_s}{P_T}R_s+R_T \right)|k \right\}\\ &=\sum_kP_TP_s^k\left[ E_\left\{ r \right\}\left\{ \sum_{i=1}^k\left( r_{s_i}^2-R_{s}^2 \right)+\left( r_{T}^2-R_{T}^2 \right)|k \right\} +k^2R_s^2+2kR_sR_T\\ +\frac{P_s^2}{P_T^2}R_s^2+R_T^2+2\frac{P_s}{P_T}R_sR_T-2k\frac{P_s}{P_T}R_s^2-2\frac{P_s}{P_T}R_sR_T-R_T^2-2kR_sR_T \right]\\ &=\sum_kP_TP_s^k\left[ k{\textrm{Var}}\left( r_s \right)+{\textrm{Var}}\left( r_T \right)+R_s^2\left( k-\frac{P_s}{P_T} \right)^2 \right]\\ &=\frac{P_s}{P_T^2}R_s^2+{\textrm{Var}}\left( r_T \right)+\frac{P_s}{P_T}{\textrm{Var}}\left( r_s \right) \end{align*}$

第一项是由于对状态 $s$ 的重访次数的变化引起的方差，第二项是由于随机奖励引起的方差。在 $n$ 次试验后首次访问MC方法估计是 $n$ 次独立试验样本的平均值，因此， ${\textrm{Var}}_n^F\left( s \right)=\frac{{\textrm{Var}}_1^F\left( s \right)}{n}$ 。

定理6 首次访问MC方法的MSE是 ${\textrm {MSE}}_n^F\left( s \right)=\left( {\textrm{Bias}}_n^F\left( s \right) \right)^2+{\textrm{Var}}_n^F\left( s \right)=\frac{1}{n}\left[ {\textrm{Var}}\left( r_T \right)+\frac{P_s}{P_T}{\textrm{Var}}\left( r_s \right)+\frac{P_s}{P_T^2}R_s^2 \right]$

定理7 一次试验后每次访问MC方法的方差受到以下限制：
${\textrm{Var}}\left( r_s \right)\left[ \frac{P_s}{3P_T}-\frac{1}{6} \right]+{\textrm{Var}}\left( r_T \right)+\frac{1}{4}\frac{P_s}{P_T^2}R_s^2\leq {\textrm{Var}}_1^E\left( s \right)$
${\textrm{Var}}_1^E\left( s \right)\leq {\textrm{Var}}\left( r_s \right)\left[ \frac{P_s}{3P_T} \right]+{\textrm{Var}}\left( r_T \right)+\frac{1}{4}\frac{P_s}{P_T^2}R_s^2$

证明：

$\begin{align*} {\textrm{Var}}_1^E\left( s \right)&=E_\left\{ x \right\}\left\{ \left( t\left( \left\{ x \right\} \right)-E\left\{ t\left( \left\{ x \right\} \right) \right\} \right)^2 \right\}\\ &=\sum_\left\{ x \right\}P\left( \left\{ x \right\} \right)\left[ \frac{r_{s_1}+2r_{s_2}+...+kr_{s_k}+\left( k+1 \right)r_T}{k+1}-\left( \frac{P_s}{2P_T}R_s+R_T \right) \right]^2\\ &=\sum_kP\left( k \right)E_\left\{ r \right\}\left\{ \sum_{i=1}^k \left( \frac{i^2}{\left( k+1 \right)^2}r_{s_i}^2+2\frac{i}{k+1}r_{s_i}r_T\right)+r^2_T\\ +\sum_{i \ne j}\frac{2ij}{\left( k+1 \right)^2}r_{s_i}r_{s_j}+\frac{P_s^2}{4P_T^2}R_s^2+\frac{P_s}{P_T}R_sR_T+R_T^2\\-2\sum_{i=1}^k\frac{i}{k+1}r_{s_i}\left( \frac{P_s}{2P_T}R_s+R_T \right)-2\frac{P_s}{2P_T}R_sr_T-2R_Tr_T|k \right\}\\ &=\sum_kP_TP_s^k\left[ {\textrm{Var}}\left( r_T \right)+\frac{k\left( 2k+1 \right)}{6\left( k+1 \right)}{\textrm{Var}}\left( r_s \right)+\frac{R_s^2}{4}\left( k-\frac{P_s}{P_T} \right)^2 \right]\\ &={\textrm{Var}}\left( r_T \right)+\frac{R_s^2}{4}\frac{P_s}{P_T^2}+{\textrm{Var}}\left( r_s \right)\sum_kP_TP_s^k\frac{k\left( 2k+1 \right)}{6\left( k+1 \right)} \end{align*}$

注意， $\frac{k}{3}-\frac{1}{6}\leq\frac{k\left( 2k+1 \right)}{6\left( k+1 \right)}=\frac{k}{3}-\frac{k}{6\left( k+1 \right)}\leq\frac{k}{3}$ 。

因此，

${\textrm{Var}}\left( r_s \right)\left[ \frac{P_s}{3P_T}-\frac{1}{6} \right]+{\textrm{Var}}\left( r_T \right)+\frac{1}{4}\frac{P_s}{P_T^2}R_s^2\leq {\textrm{Var}}_1^E\left( s \right)$

${\textrm{Var}}_1^E\left( s \right)\leq {\textrm{Var}}\left( r_s \right)\left[ \frac{P_s}{3P_T} \right]+{\textrm{Var}}\left( r_T \right)+\frac{1}{4}\frac{P_s}{P_T^2}R_s^2$

定理8 一次试验后， ${\textrm{MSE}}_1^E\left( s \right)\leq{\textrm{MSE}}_1^F\left( s \right)$ ，因为 $\left( {\textrm{Bias}}_1^E\left( s \right) \right)^2+{\textrm{Var}}_1^E\left( s \right)\leq{\textrm{MSE}}_1^F\left( s \right)$

定理9 存在 $N<\infty$ ，使得，对于所有的 $n \geq N$ ， ${\textrm{Var}}_n^E\left( s \right)\geq{\textrm{Var}}_n^F\left( s \right)$
推论存在 $N<\infty$ ，使得，对于所有的 $n \geq N$ ， ${\textrm{MSE}}_n^E\left( s \right)=\left( {\textrm{Bias}}_n^E\left( s \right) \right)^2+{\textrm{Var}}_n^F\left( s \right)\geq{\textrm{MSE}}_n^F\left( s \right)={\textrm{Var}}_n^F\left( s \right)$

图3显示了MSE发生交叉的实例。在 $N = 5$ 时发生交叉。通常，交叉可以在一次试验时发生。例如，如果问题中唯一的非零奖励是终止，则 $R_s = 0$ ， ${\textrm{Var}}\left( r_s \right)=0$ ，这反过来暗示 ${\textrm{Bias}}_n^E=0$ ，对于所有 $n$ ， ${\textrm{Var}}_1^E\left( s \right)={\textrm{Var}}_1^F\left( s \right)$ ，因此 ${\textrm{MSE}}_1^E\left( s \right)={\textrm{MSE}}_1^F\left( s \right)$ 。

证明：

对于每次访问蒙特卡洛估计， $V_n^E\left( s \right)=\frac{{\sum_{i=1}^n}t_{num}\left( \left\{ x \right\}^i \right)}{{\sum_{i=1}^n}\left( k_i+1 \right)}$

重写为， $V_n^E\left( s \right)=\frac{\frac{1}{n}\frac{\sum_{i=1}^nt_{num}\left( \left\{ x \right\}^i \right)}{E\left\{ \left( k_i+1 \right) \right\}}}{\frac{1}{n}\frac{\sum_{i=1}^n \left( k_i+1 \right)}{E\left\{ \left( k_i+1 \right) \right\}}}=\frac{\frac{1}{n}\sum_{i=1}^nP_Tt_{num}\left( \left\{ x \right\}^i \right)}{\frac{1}{n}\sum_{i=1}^nP_T\left( k_i+1 \right)}$

因为，对于所有的 $i$ ， $E\left\{ \left( k_i+1 \right) \right\}=\frac{1}{P_T}$ ，并且， $E\left\{ P_Tt_{num}\left( \left\{ x \right\}^i \right) \right\}=V\left( s \right)$ ， $E\left\{ P_T\left( k_i+1 \right) \right\}=1$ 。

考虑一个方程，

$f_n\left( \delta \right)=\frac{V\left( s \right)+\delta{\overline T}_n}{1+\delta {\overline K}_n}$

其中，

${\overline T}_n=\frac{1}{\sqrt n}\sum_{i=1}^n\left( P_Tt_{num}\left( \left\{ x \right\}^i \right)-V\left( s \right) \right)$

${\overline K}_n=\frac{1}{\sqrt n}\sum_{i=1}^n\left( P_T\left( k_i+1 \right)-1 \right)$

值得注意的是，

$\forall n,E\left( {\overline T}_n \right)=0,E\left( {\overline K}_n \right)=0$

$f_n\left( \frac{1}{\sqrt n} \right)=V_n^E\left( s \right)$

因此， ${\textrm {Var}}_n^E\left( s \right)=E\left\{ \left( f_n\left( \frac{1}{\sqrt n} \right) \right)^2 \right\}-\left( E\left\{ V_n^E\left( s \right) \right\} \right)^2$

利用泰勒展开，

$f_n^2\left( \frac{1}{\sqrt n} \right)=f_n^2\left( 0 \right)+\frac{1}{\sqrt n}\frac{\partial}{\partial \delta}f_n^2\left( \delta \right)|_{\delta=0}+ \frac{1}{n2!}\frac{\partial^2}{\partial \delta^2}f_n^2\left( \delta \right)|_{\delta=0}+\frac{1}{n^{\frac{3}{2}}3!}\frac{\partial^3}{\partial \delta^3}f_n^2\left( \delta \right)|_{\delta=0}+...$

因此，

${\textrm {Var}}_n^E\left( s \right)=E\left\{ f_n^2\left( 0 \right)+\frac{1}{\sqrt n}\frac{\partial}{\partial \delta}f_n^2\left( \delta \right)|_{\delta=0}+ \frac{1}{n2!}\frac{\partial^2}{\partial \delta^2}f_n^2\left( \delta \right)|_{\delta=0} \right\}\\+E\left\{ \frac{1}{6n^{\frac{3}{2}}}\frac{\partial^3}{\partial \delta^3}f_n^2\left( \delta \right)|_{\delta=0} +...\right\}-\left( E\left\{ V_n^E\left( s \right) \right\} \right)^2$

我们将在下面证明， $E\left\{ \frac{1}{6n^{\frac{3}{2}}}\frac{\partial^3}{\partial \delta^3}f_n^2\left( \delta \right)|_{\delta=0} +...\right\}$ 是 ${\cal O}\left( \frac{1}{n^{\frac{3}{2}}} \right)$

对于所有的 $i\geq2$ ， $E\left( \frac{\partial^2}{\partial \delta^2}f_n^2\left( \delta \right)|_{\delta=0} \right)$ 是 ${\cal O}\left( 1 \right)$

${\cal O}\left( \frac{1}{n^{\frac{3}{2}}} \right)$ 的部分即可省略，因为 ${\textrm {Var}}_n^F\left( s \right)$ 衰减为 $\frac{1}{n}$ ，所以对于一个较大的 $N$ 而言，对于所有的 $n>N$ ， ${\textrm {Var}}_n^E\left( s \right)\geq{\textrm {Var}}_n^F\left( s \right)$

我们将利用以下的事实，除fact 12外不给出证明

fact 5 $E\left\{ f_n^2\left( 0 \right) \right\}=V^2\left( s \right)$

fact 6 $E\left\{ \frac{\partial}{\partial \delta}f_n^2\left( \delta \right)|_{\delta=0} \right\}=0$ 因为 $\frac{\partial}{\partial \delta}f_n^2\left( \delta \right)|_{\delta=0}=2V\left( s \right)\left( {\overline T_n}-V\left( s \right){\overline K}_n \right)$

fact 7 $\frac{\partial^2}{\partial \delta^2}f_n^2\left( \delta \right)|_{\delta=0}=2{\overline T}_n^2-8V\left( s \right){\overline T}_n{\overline K}_n+6V^2\left( s \right){\overline K}_n^2$

fact 8 $E\left\{ {\overline K}_n^2 \right\}=P_s$

fact 9 $E\left\{ {\overline K}_n{\overline T}_n \right\}=\frac{2P_s+P_s^2}{P_T}R_s+R_T\left( P_s+1 \right)-V\left( s \right)$

fact 10 $\begin{align*} E\left\{ {\overline T}_n^2 \right\}&=\frac{P_s+P_s^2}{P_T}{\textrm{Var}}\left( r_s \right)+\left( P_s+1 \right){\textrm{Var}}\left( r_T \right)-V^2\left( s \right)\\ &+\left( P_s+1 \right)R_T^2+\frac{4P_s+2P_s^2}{P_T}R_sR_T+\frac{P_s+4P_s^2+P_s^3}{P_T^2}R_s^2 \end{align*}$

fact 11 $V^2\left( s \right)-\left( E\left\{ V_n^E\left( s \right) \right\} \right)^2=\frac{\left( 2n+1 \right)P_s^2}{\left( n+1 \right)^2P_T^2}R_s^2+\frac{2P_s}{\left( n+1 \right)P_T}R_sR_T$

fact 12 $\begin{align*} E\left\{ \frac{1}{2n}\frac{\partial^2}{\partial \delta^2}f_n^2\left( \delta \right)|_{\delta=0} \right\}&=\frac{P_s+P_s^2}{nP_T}{\textrm{Var}}\left( r_s \right)+\frac{\left( P_s+1 \right)}{n}{\textrm{Var}}\left( r_T \right)\\ &+\frac{P_s-P_s^2}{nP_T^2}R_s^2-\frac{2P_s}{nP_T}R_sR_T \end{align*}$

因此，每次访问MC估计的方差的行为是 ${\cal O}\left( \frac{1}{n} \right)$

${\textrm{Var}}_n^E\left( s \right)\approx \frac{P_s+P_s^2}{nP_T}{\textrm{Var}}\left( r_s \right)+\frac{\left( P_s+1 \right)}{n}{\textrm{Var}}\left( r_T \right)+\frac{P_s}{nP_T^2}R_s^2+\frac{n^2-n-1}{n\left( n+1 \right)^2}\frac{P_s^2}{P_T^2}R_s^2$

对比，

${\textrm{Var}}_n^F\left( s \right)=\frac{P_s}{nP_T}{\textrm{Var}}\left( r_s \right)+\frac{1}{n}{\textrm{Var}}\left( r_T \right)+\frac{P_s}{nP_T^2}R_s^2$

给出fact 12的证明：

$\begin{align*} E\left\{ \frac{1}{2n}\frac{\partial^2}{\partial \delta^2}f_n^2\left( \delta \right)|_{\delta=0} \right\}=\frac{E\left\{ 2{\overline T}_n^2-8V\left( s \right){\overline T}_n{\overline K}_n+6V^2\left( s \right){\overline K}_n^2 \right\}}{2n} \end{align*}$

由fact 10得到，

$\begin{align*} E\left\{ 2{\overline T}_n^2 \right\}&= 2\frac{P_s+P_s^2}{P_T}{\textrm{Var}}\left( r_s \right) +2\left( P_s+1 \right){\textrm{Var}}\left( r_T \right) -2V^2\left( s \right)\\ &+2\left( P_s+1 \right)R_T^2+2\frac{4P_s+2P_s^2}{P_T}R_sR_T+2\frac{P_s+4P_s^2+P_s^3}{P_T^2}R_s^2\\ &=2\frac{P_s+P_s^2}{P_T}{\textrm{Var}}\left( r_s \right) +2\left( P_s+1 \right){\textrm{Var}}\left( r_T \right) -2V^2\left( s \right)\\ &+2\left( 1+P_s \right)R_T^2+4\frac{P_s}{P_T}\left( 2+P_s \right)R_sR_T+2\frac{P_s}{P_T^2}R_s^2+8\frac{P_s^2}{P_T^2}R_s^2+2\frac{P_s^3}{P_T^2}R_s^2\\ &=2\frac{P_s+P_s^2}{P_T}{\textrm{Var}}\left( r_s \right) +2\left( P_s+1 \right){\textrm{Var}}\left( r_T \right) -2V^2\left( s \right)\\ &+2\left( 1+P_s \right)R_T^2+4\frac{P_s}{P_T}\left( 1+P_s \right)R_sR_T\\ &+4\frac{P_s}{P_T}R_sR_T+2\frac{P_s}{P_T^2}R_s^2+8\frac{P_s^2}{P_T^2}R_s^2+2\frac{P_s^3}{P_T^2}R_s^2\\ &=2\frac{P_s+P_s^2}{P_T}{\textrm{Var}}\left( r_s \right) +2\left( P_s+1 \right){\textrm{Var}}\left( r_T \right) -2V^2\left( s \right)\\ &+2\left( 1+P_s \right)\left( R_T^2+2\frac{P_s}{P_T}R_sR_T \right) \\ &+4\frac{P_s}{P_T}R_sR_T+2\frac{P_s}{P_T^2}R_s^2+2\frac{P_s^2}{P_T^2}R_s^2\left( 3+1+P_s \right)\\ &=2\frac{P_s+P_s^2}{P_T}{\textrm{Var}}\left( r_s \right) +2\left( P_s+1 \right){\textrm{Var}}\left( r_T \right) -2V^2\left( s \right)\\ &+2\left( 1+P_s \right)\left( R_T^2+2\frac{P_s}{P_T}R_sR_T+\frac{P_s^2}{P_T^2}R_s^2 \right)\\ &+\frac{4P_s}{P_T}R_sR_T+\frac{2P_s}{P_T^2}R_s^2+\frac{6P_s^2}{P_T^2}R_s^2\\ &=2\frac{P_s+P_s^2}{P_T}{\textrm{Var}}\left( r_s \right)+2\left( P_s+1 \right){\textrm{Var}}\left( r_T \right)\\ &+2P_sV^2\left( s \right)+\frac{4P_s}{P_T}R_sR_T+\frac{2P_s}{P_T^2}R_s^2+\frac{6P_s^2}{P_T^2}R_s^2 \end{align*}$

由fact 9得到，

$\begin{align*} E\left\{ -8V\left( s \right){\overline K}_n{\overline T}_n \right\} &=-8V\left( s \right)\frac{2P_s+P_s^2}{P_T}R_s+\left( -8V\left( s \right) \right)R_T\left( P_s+1 \right)-\left( -8V\left( s \right) \right)V\left( s \right)\\ &=-8V\left( s \right)\frac{P_s}{P_T}\left( 2+P_s \right)R_s-8V\left( s \right)R_TP_s-8V\left( s \right)R_T+8V^2\left( s \right)\\ &=-16V\left( s \right)\frac{P_s}{P_T}R_s-8V\left( s \right)\frac{P_s^2}{P_T}R_s\\&-8V\left( s \right)R_TP_s-8V\left( s \right)R_T+8V^2\left( s \right)\\ &=-8V\left( s \right)\left( \frac{P_s}{P_T}R_s+\frac{P_s}{P_T}R_s+\frac{P_s^2}{P_T}R_s+R_TP_s+R_T-V\left( s \right) \right)\\ &=-8V\left( s \right)\left( \frac{P_s}{P_T}R_s+\frac{P_s}{P_T}R_s\left( 1+P_s \right)+R_T\left( 1+P_s \right)-V\left( s \right) \right)\\ &=-8V\left( s \right)\left( \frac{P_s}{P_T}R_s+\left( 1+P_s \right)\left( \frac{P_s}{P_T}R_s+R_T \right)-V\left( s \right) \right)\\ &=-8V^2\left( s \right)P_s-\frac{8P_s^2}{P_T^2}R_s^2-\frac{8P_s}{P_T}R_sR_T \end{align*}$

由fact 8得到，

$E\left\{ 6V^2\left( s \right){\overline K}_n^2 \right\}=6V^2\left( s \right)P_s$

因此，

$\begin{align*} E\left\{ \frac{1}{2n}\frac{\partial^2}{\partial \delta^2}f_n^2\left( \delta \right)|_{\delta=0} \right\}&=\frac{E\left\{ 2{\overline T}_n^2-8V\left( s \right){\overline T}_n{\overline K}_n+6V^2\left( s \right){\overline K}_n^2 \right\}}{2n}\\ &={\frac{1}{2n}}E\left\{ 2{\overline T}_n^2 \right\}+{\frac{1}{2n}}E\left\{ -8V\left( s \right){\overline K}_n{\overline T}_n \right\}+{\frac{1}{2n}}E\left\{ 6V^2\left( s \right){\overline K}_n^2 \right\}\\ &={\frac{1}{2n}}\left( 2\frac{P_s+P_s^2}{P_T}{\textrm{Var}}\left( r_s \right)+2\left( P_s+1 \right){\textrm{Var}}\left( r_T \right)\\+2P_sV^2\left( s \right)+\frac{4P_s}{P_T}R_sR_T+\frac{2P_s}{P_T^2}R_s^2+\frac{6P_s^2}{P_T^2}R_s^2 \right)\\ &+{\frac{1}{2n}}\left( -8V^2\left( s \right)P_s-\frac{8P_s^2}{P_T^2}R_s^2-\frac{8P_s}{P_T}R_sR_T \right)\\ &+{\frac{1}{2n}}\left( 6V^2\left( s \right)P_s \right)\\ &=\frac{P_s+P_s^2}{nP_T}{\textrm{Var}}\left( r_s \right)+\frac{ 1+P_s}{n}{\textrm{Var}}\left( r_T \right)+\cancel{\frac{P_s}{n}V^2\left( s \right)}+\frac{2P_s}{nP_T}R_sR_T\\&+\frac{P_s}{nP_T^2}R_s^2+\frac{3P_s^2}{nP_T^2}R_s^2-\cancel{\frac{4P_s}{n}V^2\left( s \right)}\\&-\frac{4P_s^2}{nP_T^2}R_s^2-\frac{4P_s}{nP_T}R_sR_T+\cancel{\frac{3P_s}{n}V^2\left( s \right)}\\ &=\frac{P_s+P_s^2}{nP_T}{\textrm{Var}}\left( r_s \right)+\frac{ 1+P_s}{n}{\textrm{Var}}\left( r_T \right)\\&+\frac{P_s}{nP_T^2}R_s^2-\frac{P_s^2}{nP_T^2}R_s^2-\frac{2P_s}{nP_T}R_sR_T\\ &=\frac{P_s+P_s^2}{nP_T}{\textrm{Var}}\left( r_s \right)+\frac{ 1+P_s}{n}{\textrm{Var}}\left( r_T \right)\\&+\frac{P_s-P_s^2}{nP_T^2}R_s^2-\frac{2P_s}{nP_T}R_sR_T \end{align*}$

小结

参考文献：

【1】Reinforcement Learning with Replacing Eligibility Traces

请大家批评指正，谢谢～

编辑于 2019-01-05

「真诚赞赏，手留余香」

还没有人赞赏，快来当第一个赞赏的人吧！

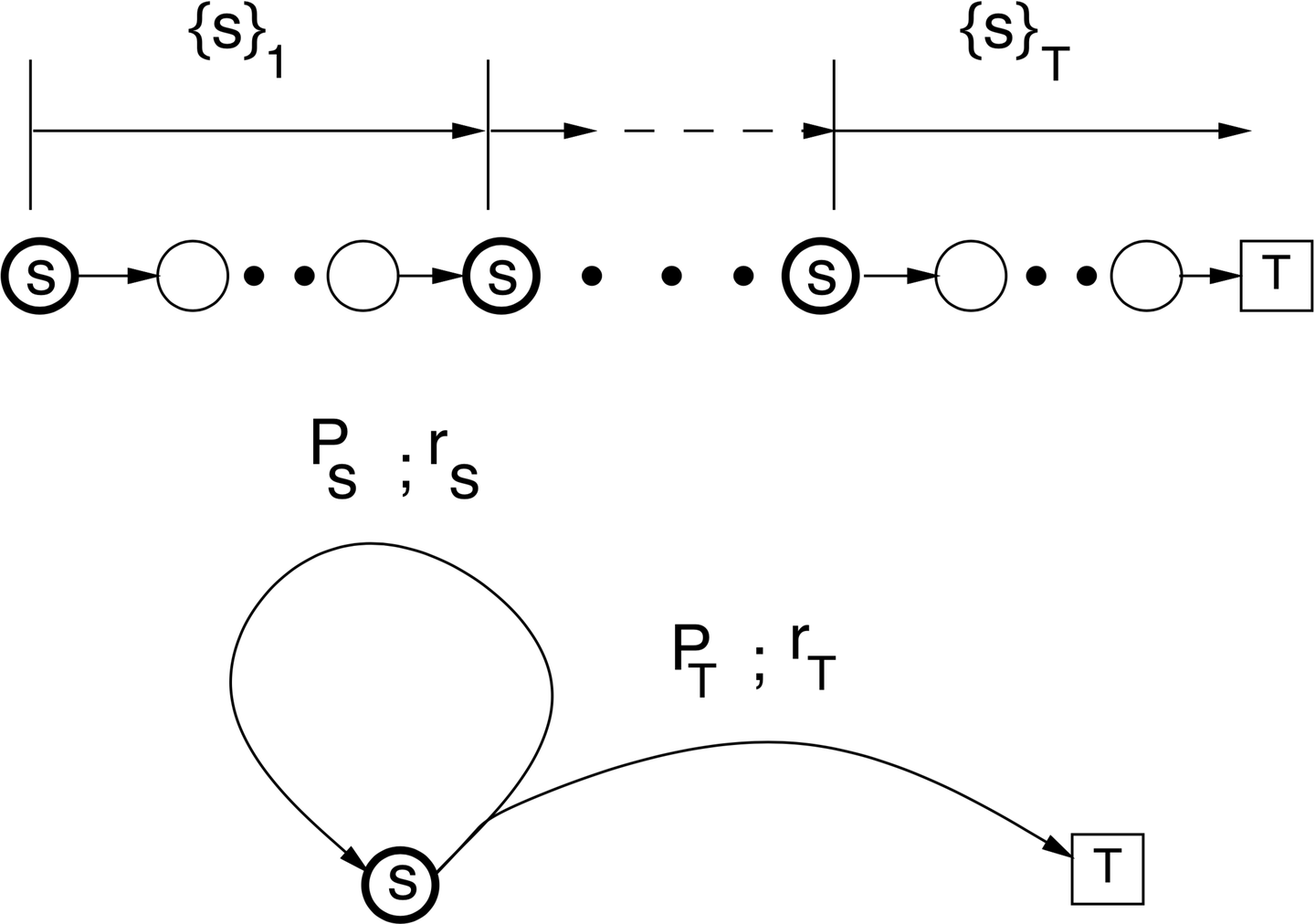
强化学习——每次访问MC方法和首次访问MC方法的相关理论证明

前言

示例——首次访问MC方法和每次访问MC方法的区别

简化的双状态抽象马尔可夫链

首次访问MC方法 first-visit MC

每次访问MC方法 every-visit MC

相关概念说明

小结

文章被以下专栏收录

旺财的搬砖历险记

推荐阅读

多智能体连续行为空间问题求解——MADDPG

【强化学习算法 15】h-DQN

强化学习（十三）--AC、A2C、A3C算法

理解强化学习知识之解决无模型的MDP

4 条评论

前言

示例——首次访问MC方法和每次访问MC方法的区别

简化的双状态抽象马尔可夫链

首次访问MC方法 first-visit MC

每次访问MC方法 every-visit MC

相关概念说明

小结

文章被以下专栏收录

旺财的搬砖历险记

推荐阅读

多智能体连续行为空间问题求解——MADDPG

【强化学习算法 15】h-DQN

强化学习（十三 ）--AC、A2C、A3C算法

理解强化学习知识之解决无模型的MDP

4 条评论

强化学习（十三）--AC、A2C、A3C算法