1. 从最优化引出的拉格朗日乘数法
1.1 一个最简单的无约束优化问题
在学习与工程之中,我们时常会遇到一些优化的问题,也就是要对某个目标函数求取极值,最简单的形式如下。
min x ∈ R n f ( x ) \large \min_{x \in \mathbb{R^n}}{f(x)} x∈Rnminf(x)
这个式子表达的含义是以 x x x 为自变量,求取 f ( x ) f(x) f(x) 的最小值。如果想要求取最大值,可以把 f f f 加一个符号,这样把 max x f ( x ) \max_{x}{f(x)} maxxf(x) 转换为等价的 min x − f ( x ) \min_{x}{-f(x)} minx−f(x) 就行了。另外需要注意的是 x x x 并非一个标量数值,而是n维实数空间上的一个向量。
这样的例子有很多,最常见的就比如我们在机器学习中经常碰到的最小化代价函数。对于这样的问题,我们求解的方法很简单,只要能够求出一个点 x ′ x^\prime x′,使得 ∇ f ( x ′ ) = 0 \nabla f(x^\prime) = 0 ∇f(x′)=0 即可。
当然我们也知道,只有当 f f f 是凸函数的时候,这样求出来的才是全局最优点,否则不过是个局部最优点罢了。不过这就不在我们的讨论范围内了。现在我们姑且假定讨论的 f f f 都是凸函数。
1.2 带有等式约束的优化问题
我们在上一节的基础上进一步,如果 f f f 是有约束的呢?
min
x
∈
R
n
f
(
x
)
s
.
t
h
i
(
x
)
=
0
,
i
∈
[
1
,
l
]
\large
在这个问题中,我们对在定义域上的 x x x 有了 l l l 个等式约束 h i h_i hi。这样一来我们就不能随意的计算导数等于0的点作为最优点了。那要怎么做呢?
这时就需要用到拉格朗日乘数法了,具体而言,我们首先来构建这么一个拉格朗日函数:
L
(
x
,
λ
)
=
f
(
x
)
+
∑
i
=
1
l
λ
i
h
i
(
x
)
x
∈
R
n
,
λ
∈
R
l
这里
λ
\lambda
λ 是新引入的参数,被称为拉格朗日乘子,在这里它是一个
l
l
l 维的向量。
接着我们需要求解方程:
{
∂
L
∂
x
=
0
h
i
(
x
)
=
0
\left\{
求解出来的结果 x ′ x^\prime x′ 必然就是最大值或最小值对应的点,只要稍加检验就可以得出结果了。
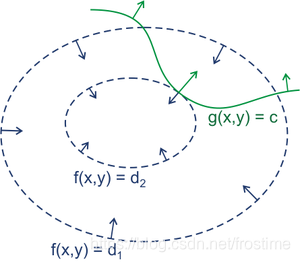
那么为什么会这样呢?这里我们稍加解释,如下图所示, f ( x , y ) f(x, y) f(x,y) 是我们的目标函数 f ( x ) f(x) f(x),而 g ( x , y ) g(x, y) g(x,y) 则是我们的约束条件 h ( x ) h(x) h(x)。
显然我们的目标就是求出在 f f f 和 g g g 的交点上的最小值。稍加思索,我们不难发现,这样的点一定是两个 g g g 和 f f f 的某个等高线相切的一个点。原因很简单:假定我们的目标 x ∗ x^* x∗ 不是切点,那么它必然可以沿着负梯度的方向朝着更低的方向前进,那这就意味着它必然不是最小值对应的点。
所以我们就有结论:
若 x ∗ x^* x∗ 是被等式 h h h 约束的最优化问题 min f \min f minf 的解,则 f f f 和 h h h 在 x ∗ x^* x∗ 处相切
既然
f
f
f 和
h
h
h 在
x
∗
x^*
x∗ 上相切,那就意味着二者在这一点的梯度的方向相同,即:
∇
f
=
λ
∇
h
,
λ
≠
0
\nabla f = \lambda \nabla h,\quad \lambda \not = 0
∇f=λ∇h,λ=0
稍加整理,我们就可以得出结论,只要
x
x
x 满足:
{
d
f
d
x
+
λ
d
h
d
x
=
0
h
(
x
)
=
0
\left\{
那么
x
x
x 就是我们希望的最优点。稍加整理就是上面的拉格朗日函数的形式了。
更详细的解释见这里。
1.3 再加上不等式约束
然而实际生活中我们可能碰到的问题比上面的还要复杂,不仅仅是有等式约束,还可能会有不等式约束。
现在假定
f
(
x
)
,
c
i
(
x
)
,
h
i
(
x
)
f(x),\ c_i(x),\ h_i(x)
f(x), ci(x), hi(x) 都是定义在
R
n
\mathbb{R^n}
Rn 上的连续可微函数,则考虑约束最优化问题:
min
x
∈
R
n
f
(
x
)
s
.
t
c
i
(
x
)
⩽
0
,
i
∈
[
1
,
k
]
h
j
(
x
)
=
0
,
j
∈
[
1
,
l
]
(1)
\large
式(1)就是我们实际会遇到的优化问题的基本形式。如何求解这个优化问题也就是这篇文章主要要探讨的。
关于具体如何求解,我们从第三节再开始讲其。第二节中,我们主要先把一些需要用到的数学概念理清了。
2. 预备的数学知识
2.1 数学符号说明
min \min min/ max \max max 符号
在接下来你会看到一大堆这样:
min
x
f
(
x
)
(a)
\min_{x} f(x) \tag{a}
xminf(x)(a)
这样的:
max
x
∈
D
f
(
x
,
λ
)
(b)
\max_{x \in D}f(x, \lambda) \tag{b}
x∈Dmaxf(x,λ)(b)
甚至这样的:
max
λ
min
x
f
(
x
,
λ
)
(c)
\max_{\lambda}\min_{x}f(x, \lambda) \tag{c}
λmaxxminf(x,λ)(c)
所以如果不把
min
x
\min_x
minx 或者
max
x
\max_x
maxx 这个符号搞清楚的话,接下来可能会很难受。
简而言之,式子(a)的意思是对于函数 f ( x ) f(x) f(x) ,考察 x x x (可以理解为改变 x x x),来找到它的最小值。有时候在 min \min min 的下标的位置还会带上一些限制条件,比如(b)中的 x ∈ D x \in D x∈D,意思就是“考察在集合 D 中的 x x x”。
这个符号的含义在函数只有一个自变量
x
x
x 的时候倒不会出现什么混淆,但是当自变量不止一个的时候就容易弄混了。来我们来看看式子(b):
max
x
∈
D
f
(
x
,
λ
)
(b)
\max_{x \in D}f(x, \lambda) \tag{b}
x∈Dmaxf(x,λ)(b)
函数
f
f
f 是一个关于
x
,
λ
x, \lambda
x,λ 两个变量的函数。所以式子(b)的含义就是固定
λ
\lambda
λ 不变,改变
x
x
x 从而使得
f
f
f 的值最大。有时候可能会看到这样的格式:
g
(
λ
)
=
max
x
∈
D
f
(
x
,
λ
)
g(\lambda) = \max_{x \in D}f(x, \lambda)
g(λ)=x∈Dmaxf(x,λ)
这个式子的意思是:
- g ( λ ) g(\lambda) g(λ) 是一个关于 λ \lambda λ 的函数
- 当 λ = y \lambda = y λ=y 时, g ( λ ) g(\lambda) g(λ) 的取值为:固定 f ( x , λ ) f(x, \lambda) f(x,λ) 中的 λ = y \lambda = y λ=y,变动 x x x 时 f f f 能取到的最大值
比如:
f
(
x
,
y
)
=
x
2
+
y
2
g
(
y
)
=
min
x
∈
D
f
(
x
,
y
)
g
(
4
)
=
min
x
∈
D
f
(
x
,
4
)
=
min
x
∈
D
(
x
2
+
16
)
=
0
+
16
=
16
在进一步,有时候
min
\min
min 还有
max
\max
max 会像©一样叠加在一起:
v
=
max
λ
min
x
f
(
x
,
λ
)
v = \max_{\lambda}\min_{x}f(x, \lambda)
v=λmaxxminf(x,λ)
这个式子要从右往左看,首先把
min
x
f
(
x
,
λ
)
\min_{x}f(x, \lambda)
minxf(x,λ) 这一项理解成关于
λ
\lambda
λ 的函数
g
(
λ
)
g(\lambda)
g(λ),然后再对
g
g
g 求最大值,即:
g
(
λ
)
=
min
x
f
(
x
,
λ
)
v
=
max
λ
g
(
λ
)
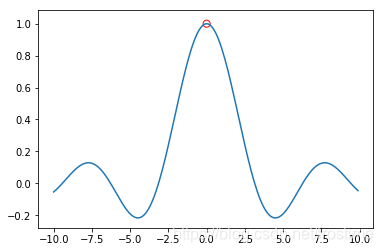
inf \inf inf 和 sup \sup sup 符号
inf \inf inf 是 infimum (下确界) 的简称,而 sup \sup sup 是 supremum (上确界) 的简称。它们和 min 还有 max 很相似,但是细节部分略有不同。具体来讲,一个例子足以:
有函数 f ( x ) = s i n ( x ) x \large f(x) = \frac{sin(x)}{x} f(x)=xsin(x):
显然 f f f 在 0 处没有定义。那么:
- max f \max{f} maxf 不存在
- sup f \sup{f} supf 存在,且为1
其他符号
- d o m f dom\ f dom f: 函数 f f f 的定义域
- ⋂ S i \bigcap S_i ⋂Si: 对若干集合 S i S_i Si 求交集
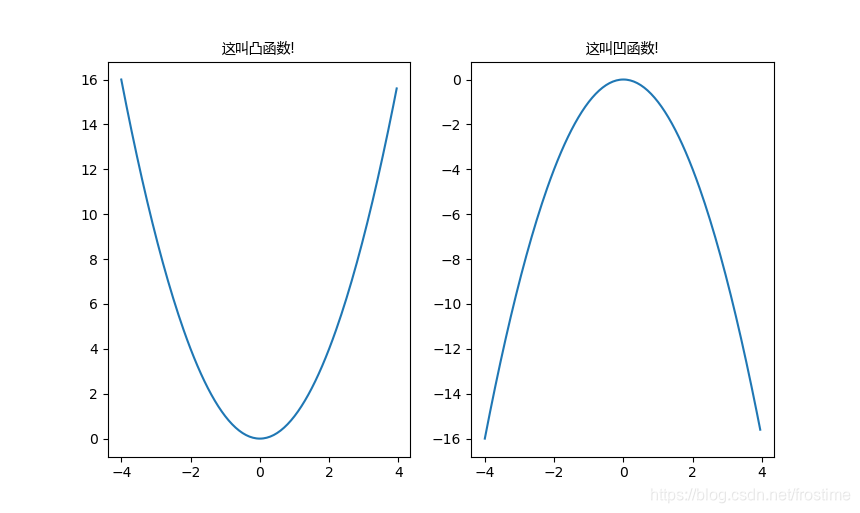
2.2 凸函数和凹函数
关于这两个,我有一言请诸位静听:
没错,其实是上凹下凸,这是国际惯例,我们国内的定义(也就是中学教的)是反过来的,我们在此后一律使用国际标准。
另外关于凸函数和凹函数有性质如下:
- 若函数 f : R n → R f: \mathbb{R^n} \to \mathbb{R} f:Rn→R 是凸的,则:
∀
x
,
y
∈
d
o
m
f
,
∀
θ
∈
[
0
,
1
]
f
(
θ
x
+
(
1
−
θ
)
y
)
⩽
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
- 若函数 f : R n → R f: \mathbb{R^n} \to \mathbb{R} f:Rn→R 是凹的,则:
∀
x
,
y
∈
d
o
m
f
,
∀
θ
∈
[
0
,
1
]
f
(
θ
x
+
(
1
−
θ
)
y
)
⩾
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
2.3 仿射函数
假如有 x ⃗ ∈ R n \vec{x} \in \mathbb{R^n} x∈Rn, b ⃗ ∈ R m \vec{b} \in \mathbb{R^m} b∈Rm, 矩阵 A m × n A_{m\times n} Am×n,那么:
x ⃗ → A x ⃗ + b ⃗ \vec x \rightarrow A\vec x + \vec b x→Ax+b
被称为
R
n
→
R
m
\mathbb{R^n} \rightarrow \mathbb{R^m}
Rn→Rm 的仿射变换,这一过程被称为仿射函数。
f
(
x
)
=
A
x
+
b
,
x
∈
R
n
f(x) = Ax + b,\ x\in \mathbb{R^n}
f(x)=Ax+b, x∈Rn
比如最简单的:
a
1
x
1
+
a
2
x
2
+
⋯
+
a
n
x
n
+
b
a_1x_1 + a_2x_2 + \cdots + a_nx_n + b
a1x1+a2x2+⋯+anxn+b
就是一个仿射函数。
仿射函数有一个非常重要的性质,那就是它既凹又凸,准确来讲在凹凸函数的那个不等式中,仿射函数是可以取等号的:
f
(
θ
x
+
(
1
−
θ
)
y
)
=
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
f(\theta x + (1 - \theta)y) = \theta f(x) + (1 - \theta) f(y)
f(θx+(1−θ)y)=θf(x)+(1−θ)f(y)
这个证明很简单,自己都可以试试。
2.4 凸优化
我们在 1.3 节中的式 (1) 给出的式子其实是优化问题的基本形式:
min
x
∈
R
n
f
(
x
)
s
.
t
c
i
(
x
)
⩽
0
,
i
∈
[
1
,
k
]
h
j
(
x
)
=
0
,
j
∈
[
1
,
l
]
\large
而所谓的凸优化,是满足一些特定条件的优化问题,它要求:
- f ( x ) f(x) f(x) 是凸函数
- c i ( x ) c_i(x) ci(x) 是凸函数
- h j ( x ) h_j(x) hj(x) 是仿射函数
也就是
min
x
∈
R
n
f
(
x
)
s
.
t
c
i
(
x
)
⩽
0
,
i
∈
[
1
,
k
]
a
j
x
=
b
j
,
j
∈
[
1
,
l
]
\large
凸优化有一个重要的性质:任意位置的局部最优解同时也是全局最优解。
3. 从广义拉格朗日函数到拉格朗日对偶函数
OK,做了一大堆铺垫,我们终于要开始正式将拉格朗日对偶了。
首先来回忆一下我们的原问题 (Primal Problem):
min
x
∈
R
n
f
(
x
)
s
.
t
c
i
(
x
)
⩽
0
,
i
∈
[
1
,
k
]
h
j
(
x
)
=
0
,
j
∈
[
1
,
l
]
(1)
\large
首先我们做两个约定:
- 我们不假定原函数 f f f 的凹凸性,也就是 f f f 可以是非凸非凹函数
- 记问题的定义域 D = ( d o m f ) ∩ ( ⋂ i = 1 k c i ) ∩ ( ⋂ i = 1 l h i ) D = (dom\ f)\cap(\bigcap_{i=1}^k{c_i})\cap (\bigcap_{i=1}^l{h_i}) D=(dom f)∩(⋂i=1kci)∩(⋂i=1lhi)
- D ≠ ∅ D \neq \empty D=∅
- 我们约定最终求出来的最优结果用 p ∗ p^* p∗ 表示
3.1 啥是对偶?
对于原问题(1)我们通常用拉格朗日对偶的方式来求解。啥是对偶?对偶说白了就是实质相同但从不同角度提出不同提法的一对问题。有时候原问题 (Primal Problem) 不太好解,但是对偶问题 (Dual Problem) 却很好解,我们就可以通过求解对偶问题来迂回地解答原问题。
在这里我们用的是拉格朗日对偶的方法来解决,既然我们说用对偶的方法的原因在于原问题不好解,那么这里也是如此吗?
当然了。
首先我们来看看原问题有什么难的地方:
- 约束条件太多
很显然约束越多,问题就越难解决,原问题中总共有 k + l k + l k+l 个约束,相当麻烦 - 原问题凹凸性不明确
之前我们说过,“不假定原函数 f f f 的凹凸性”,这就意味着我们无法将凸优化的方法应用在原问题中
那么它的拉格朗日对偶问题有什么优点呢?
- 只有一个约束
- 拉格朗日对偶问题一定是凹的
这里先做一个感性的认识,细节方面接下来慢慢说。
3.3 广义 Lagrange 函数
早前我们说过,对于等式约束问题可以用构建拉格朗日函数的方法来求解。这里也一样,我们可以为原问题构建一个广义拉格朗日函数 L \mathcal{L} L:
L
:
R
n
×
R
k
×
R
l
→
R
L
(
x
,
λ
,
μ
)
=
f
(
x
)
+
∑
i
=
1
k
λ
i
c
i
(
x
)
+
∑
j
=
1
l
μ
j
h
j
(
x
)
x
⃗
∈
R
n
,
λ
⃗
∈
R
k
,
μ
⃗
∈
R
l
(2)
λ
⃗
\vec \lambda
λ 和
μ
⃗
\vec \mu
μ 被称为拉格朗日乘子向量。
有了这个广义拉格朗日函数,现在我们分别可以定义另外对偶函数 g g g。
3.4 Lagrange 对偶函数 g g g
我们可以根据 L \mathcal{L} L 定义一个拉格朗日对偶函数 (Lagrange Dual Function) g ( λ , μ ) g(\lambda, \mu) g(λ,μ):
g
(
λ
,
μ
)
=
inf
x
∈
D
L
(
x
,
λ
,
μ
)
=
inf
x
∈
D
(
f
(
x
)
+
∑
i
=
1
k
λ
i
c
i
(
x
)
+
∑
j
=
1
l
μ
j
h
j
(
x
)
)
λ
⩾
0
(3)
注意到 λ ⩾ 0 \lambda \geqslant 0 λ⩾0 这个要求,为什么会有这么一个要求我们下一节讲,现在先看一些别的。
这个对偶函数 g g g 有一个非常重要的性质:它一定是一个凹函数,我们可以证明一下。
首先我们明确一个凹函数具有性质:
f
(
θ
x
+
(
1
−
θ
)
y
)
⩾
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
f(\theta x + (1 - \theta)y) \geqslant \theta f(x) + (1 - \theta) f(y)
f(θx+(1−θ)y)⩾θf(x)+(1−θ)f(y)
要证明
g
g
g 是一个凹函数就是要证明它满足这个不等式。
- 第一步
我们首先记:
g
(
λ
,
μ
)
=
inf
x
∈
D
{
L
(
x
1
,
λ
,
μ
)
,
L
(
x
2
,
λ
,
μ
)
,
⋯
,
L
(
x
n
,
λ
,
μ
)
}
,
n
→
+
∞
g(\lambda, \mu) = \inf_{x\in D}\{\mathcal{L}(x_1, \lambda, \mu), \mathcal{L}(x_2, \lambda, \mu), \cdots, \mathcal{L}(x_n, \lambda, \mu)\}, n\to +\infty
g(λ,μ)=x∈Dinf{L(x1,λ,μ),L(x2,λ,μ),⋯,L(xn,λ,μ)},n→+∞
这个好理解,就是把连续的函数离散成无限个点的集合,这样就可以把 g g g 看作一个逐点求下界的无穷集合。
- 第二步
简记:
γ
=
(
λ
,
μ
)
,
g
(
γ
)
=
g
(
λ
,
μ
)
\gamma = (\lambda, \mu),\ g(\gamma) = g(\lambda, \mu)
γ=(λ,μ), g(γ)=g(λ,μ)
这个主要是为了一会推导的时候方便写。
- 第三步
证明过程如下:
g
(
θ
γ
1
+
(
1
−
θ
)
γ
2
)
=
inf
{
L
(
x
1
,
θ
γ
1
+
(
1
−
θ
)
γ
2
)
,
L
(
x
2
,
θ
γ
1
+
(
1
−
θ
)
γ
2
)
,
⋯
,
L
(
x
n
,
θ
γ
1
+
(
1
−
θ
)
γ
2
)
}
=
inf
{
θ
L
(
x
1
,
γ
1
)
+
(
1
−
θ
)
L
(
x
1
,
γ
2
)
,
⋯
,
θ
L
(
x
n
,
γ
1
)
+
(
1
−
θ
)
L
(
x
n
,
γ
2
)
}
⩾
θ
inf
{
L
(
x
1
,
γ
1
)
,
L
(
x
2
,
γ
1
)
,
⋯
,
L
(
x
n
,
γ
1
)
}
+
(
1
−
θ
)
inf
{
L
(
x
1
,
γ
2
)
,
L
(
x
2
,
γ
2
)
,
⋯
,
L
(
x
n
,
γ
2
)
}
=
θ
g
(
γ
1
)
+
(
1
−
θ
)
g
(
γ
2
)
来逐行解释一下:
-
第一行:之前讲过了,略
-
第二行
注意到 L ( x i , γ ) \mathcal{L}(x_i, \gamma) L(xi,γ) 中, x i x_i xi 的值已经固定了, ∴ f ( x ) , c i ( x ) , h i ( x ) \therefore f(x),\ c_i(x),\ h_i(x) ∴f(x), ci(x), hi(x) 都是常数,我们分别记为 r , p , q r, p, q r,p,q。则:
L ( x i , γ ) = ∑ λ i p i + ∑ μ j q j + r \mathcal{L}(x_i, \gamma) = \sum{\lambda_i p_i} + \sum{\mu_j q_j} + r L(xi,γ)=∑λipi+∑μjqj+r
显然, L \mathcal{L} L 是一个仿射函数,而我们知道仿射函数又凸又凹,所以有:
L ( x n , θ γ 1 + ( 1 − θ ) γ 2 ) ⩾ θ L ( x n , γ 1 ) + ( 1 − θ ) L ( x n , γ 2 ) \mathcal{L}(x_n, \theta\gamma_1 + (1 - \theta)\gamma_2) \geqslant \theta \mathcal{L}(x_n, \gamma_1) + (1 - \theta) \mathcal{L}(x_n, \gamma_2) L(xn,θγ1+(1−θ)γ2)⩾θL(xn,γ1)+(1−θ)L(xn,γ2)
整理一下,就有了第二行。 -
第三行
从第二行到第三行,运用了一个简单的数学原理:
m i n { a i + b i } ⩾ m i n { a } + m i n { b } min\{a_i + b_i\} \geqslant min\{a\} + min\{b\} min{ai+bi}⩾min{a}+min{b}
总结: 不管原函数 f f f 的凹凸性,它的对偶函数 g g g 一定是凹函数
3.5 对偶函数与原函数的关系
我们之所以需要这么一个对偶函数是因为 g g g 有一个非常重要的作用,引用一句《凸优化》原文的句子:
Give the lower bound on optimal value ( p ∗ p^* p∗)
什么意思呢?其实这是 Dual Function 一个很重要的性质:
∀
λ
⩾
0
⇒
g
(
λ
,
μ
)
⩽
p
∗
(4)
\forall \lambda \geqslant 0 \Rightarrow g(\lambda, \mu) \leqslant p^* \tag{4}
∀λ⩾0⇒g(λ,μ)⩽p∗(4)
换而言之,只要
λ
\lambda
λ 不小于0,
g
g
g 的值用于不会超过
p
∗
p^*
p∗!
要证明这个定理并不难,我们首先假设 x ^ ∈ D \hat x \in D x^∈D 是原问题的一个可行解:
∵
c
i
(
x
^
)
⩽
0
,
h
i
(
x
^
)
=
0
∴
λ
i
c
i
⩽
0
,
μ
i
h
i
=
0
∴
L
(
x
^
,
λ
,
μ
)
=
f
(
x
)
+
∑
i
=
1
k
λ
i
c
i
(
x
^
)
+
∑
j
=
1
l
μ
j
h
j
(
x
^
)
⩽
f
(
x
)
Meanwhile
g
(
λ
,
μ
)
=
inf
L
,
p
∗
=
min
f
∴
g
(
λ
,
μ
)
⩽
L
⩽
p
∗
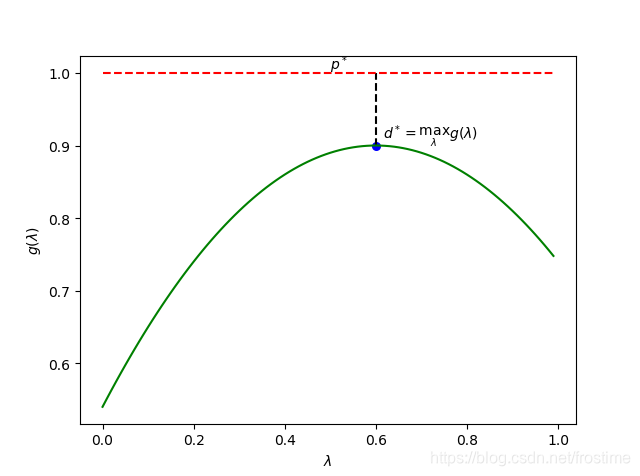
这给了我们一个重要的启示,无论如何, p ∗ p^* p∗ 都不会小于 max g ( λ , μ ) \max{g(\lambda, \mu)} maxg(λ,μ)。
4. 从原问题到拉格朗日对偶问题
在此之前,我们讲了原问题,讲了广义拉格朗日函数和拉格朗日对偶函数,又讲了这两个之间的关系。那么这有什么用呢?
用处当然很大啦!现在我们不妨这么一想,既然 Lagrange 对偶函数给出了最优解 p ∗ p^* p∗ 的下界,那么请问:
What is the best lower bound that can be obtained from lagrange dual function?
啥意思?我们来捋一捋:
- 首先我们明确一件事,我们的目的是找到最优解 p ∗ p^* p∗
- 有时候 p ∗ p^* p∗ 其实并不一定能解出来,这种情况下,我们希望可以给出一个尽可能地逼近 p ∗ p^* p∗ 的值
- 既然我们已经知道了 g g g 可以给出下界,那么那个值能够尽可能逼近呢?
- 答案是: max g ( λ , μ ) \max g(\lambda, \mu) maxg(λ,μ) ( s . t λ ⩾ 0 s.t\ \lambda \geqslant 0 s.t λ⩾0)
明白了这一点,我们终于可以介绍拉格朗日对偶问题了。
首先再次回顾一下原问题。
Primal Problem
min
x
∈
R
n
f
(
x
)
s
.
t
c
i
(
x
)
⩽
0
,
i
∈
[
1
,
k
]
h
j
(
x
)
=
0
,
j
∈
[
1
,
l
]
(1)
\large \text{Primal Problem}\\
然后隆重介绍对偶问题的形式。
Lagrange Dual Problem
max
λ
,
μ
g
(
λ
,
μ
)
=
max
λ
,
μ
inf
x
∈
D
L
(
x
,
λ
,
μ
)
s
.
t
λ
i
⩾
0
,
i
=
1
,
2
,
…
,
k
(5)
\large \text{Lagrange Dual Problem}\\
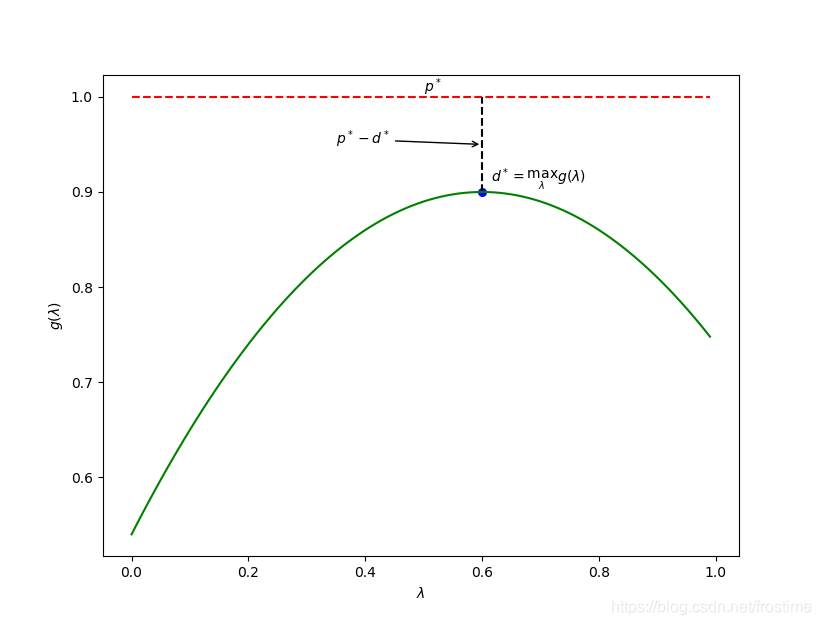
参考上面那幅图,其实这个所谓的对偶问题在干什么已经很清楚了。我们把问题 (1) 的结果令为 p ∗ p^* p∗,而问题 (5) 的结果记为 d ∗ d^* d∗。
现在回顾一下之前说的求解对偶问题的好处,我们再来看看为什么需要拉格朗日对偶。
首先是问题 (1) 有哪些 annoying 的地方:
- 原问题的约束太多了,又是等式又是不等式
- 问题 (1) 不一定是一个凸优化问题,所以即便找到了貌似是 p ∗ p^* p∗ 的点,也很可能不过是个局部最优点。
那 Lagrange 对偶问题 (5) 就好一些吗?还真是,我们来康康:
- 约束少了,这是很明显的,少了 l l l 个,而且剩下的 k k k 个约束也比原来的简单一些
- 最最重要的,问题 (5) 一定是一个凸优化问题,所以很多凸优化的手段全可以用上了
总结一下就是:
我们希望求 p ∗ p^* p∗,但是 p ∗ p^* p∗ 实在不好求,所以退而求其次去求 d ∗ d^* d∗,这个就好求多了。
并且由于 d ∗ ⩽ p ∗ d^* \leqslant p^* d∗⩽p∗,我们在求出了 d ∗ d^* d∗ 后即便不能得到 p ∗ p^* p∗,也可以得到 p ∗ p^* p∗ 的下界;而在一些非常理想的情况下, d ∗ = p ∗ d^* = p^* d∗=p∗。
d ∗ = p ∗ d^* = p^* d∗=p∗?如果真能这样那简直就是天堂了,显然一般情况下这两个是不同的,但是在满足某些特殊条件时,这个等式就可以成立了。具体这些条件是什么,我们在接下来的几节里再来谈谈。
5. 弱对偶与强对偶
5.1 弱对偶
所谓强弱对偶,指的是 Lagrange 对偶问题的一种性质,关于弱对偶我们其实在前面已经谈到了。
d ∗ ⩽ p ∗ (6) d^* \leqslant p^* \tag{6} d∗⩽p∗(6)
即便原文题不是凸问题,上述的不等式也成立,这就是所谓的弱对偶性 (Weak Dulity)。这样的性质即便是 d ∗ d^* d∗ p ∗ p^* p∗ 无限时也成立,也就是说:
- 如果 p ∗ = − ∞ p^* = -\infty p∗=−∞,则 d ∗ = − ∞ d^* = -\infty d∗=−∞
- 如果 d ∗ = + ∞ d^* = +\infty d∗=+∞,则 p ∗ = + ∞ p^* = +\infty p∗=+∞
我们还把 p ∗ − d ∗ p^* - d^* p∗−d∗ 称为最优对偶间隙 (Optimal Duality Gap),这个值必然非负。
5.2 强对偶
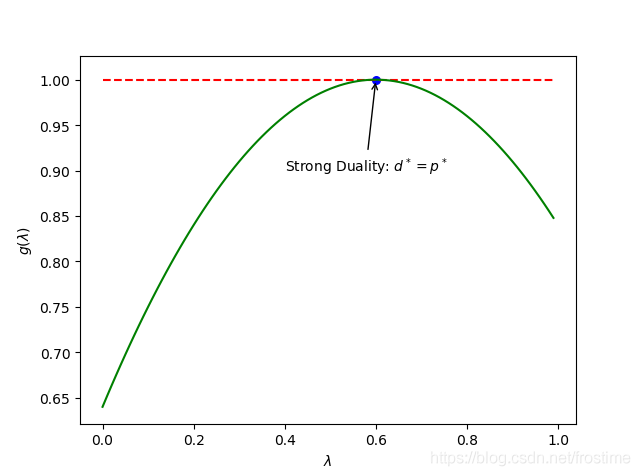
对于式子 (6) 还有一种很特殊的情况:
d ∗ = p ∗ (7) d^* = p^* \tag{7} d∗=p∗(7)
这种情况,我们称之为强对偶性 (Strong Duality)。
之所以称之为“强”对偶,正是因为这种性质相对于“弱”对偶而言对我们的意义更加重大。很显然,当我们待求解的问题是强对偶的话,那就意味着我们通过对偶问题求的的解就不再仅仅是原问题解的一个下界了,而是 p ∗ p^* p∗ 本身。用人话来讲就是:
如果满足强对偶,那只要我们求出了 d ∗ d^* d∗ ,我们就知道了 p ∗ p^* p∗ 的值
显然,强对偶并不是什么时候都成立的,必须要满足一定的条件才会有强对偶这种东西。
下一节,我们着重讲解这些条件是什么 (充分条件、必要条件)。
6. 关于强对偶和最优的一些条件
首先要明确一件事情:使满足强对偶的条件有很多种,我们这里只介绍最基本的。
6.1 Convex + Slater
如果:
- 原问题是凸优化
- 满足 Slater 条件
则一定满足强对偶
注: 这是强对偶的一个充分条件
下面具体解释一下含义。
首先是第 1 点,在 2.4 节中我们讲到过,这意味着:
- f ( x ) f(x) f(x) 是凸函数
- c i ( x ) c_i(x) ci(x) 是凸函数
- h j ( x ) h_j(x) hj(x) 是仿射函数
再来看看第 2 点,所谓的 Slater 条件。严格的 Slater 条件表述如下:
∃
x
∈
D
c
i
(
x
)
<
0
,
i
∈
[
1
,
k
]
A
x
=
b
(8)
其中
A
x
=
b
Ax = b
Ax=b 是把
a
j
x
=
b
j
a_jx=b_j
ajx=bj 合起来写的写法,我们的主要关注点在
c
i
c_i
ci 上。我们把满足该条件的点称为是严格可行的,因为不等式约束要求严格成立。
之所以称上述的 Slater 条件是严格的,是因为 Slater 还有一个弱化的版本。
若
c
i
(
x
)
是仿射函数
,
i
=
[
1
,
p
]
&
p
⩽
k
则弱化的 Slater 条件为:
∃
x
∈
D
c
i
(
x
)
⩽
0
,
i
∈
[
1
,
p
]
c
i
(
x
)
<
0
,
i
∈
[
p
+
1
,
k
]
A
x
=
b
(9)
任意满足:
- 凸优化
- 强或弱 Slater 条件
的优化问题同样满足强对偶性 (充分条件)。
6.2 KKT 条件
有必要明确一些很重要的点。
首先是 KKT 条件实际上应该分为两种情况讨论:
- Case 1: 原问题为非凸问题情况下的 KKT
- Case 2: 原问题为凸问题情况下的 KKT
为什么要分两点来讨论?因为在两种情况下,KKT 条件作为一个“条件”的充分性和必要性是不同的,自然用法也不同。
再有一个问题是,无论哪种情况,KKT 都是着眼于“最优解”这个议题进行讨论的。
下面分两种情况讨论。
6.2.1 非凸问题下的 KKT
当原问题并非凸优化(或者不清楚、不关心是不是凸优化)时,KKT 条件是一种用来描述强对偶情况下最优解性质的条件
换而言之,若强对偶性质成立,那么满足最优解的点一定满足 KKT 条件;KKT 条件是强对偶一个必要条件,但无法作为充分条件来使用
我们首先给出 KKT 条件的具体数学描述,然后逐行解释。
假设:
- 原问题中的函数均可微
- 强对偶成立
- x ∗ x^* x∗ 和 ( λ ∗ , μ ∗ ) (\lambda^*, \mu^*) (λ∗,μ∗) 分别为原问题和对偶问题的某对最优解
则:
c
i
(
x
∗
)
⩽
0
i
=
1
,
…
,
k
h
i
(
x
∗
)
=
0
i
=
1
,
…
,
l
λ
i
∗
⩾
0
i
=
1
,
…
,
k
λ
i
∗
c
i
(
x
∗
)
=
0
i
=
1
,
…
,
k
∇
f
(
x
∗
)
+
∑
i
=
1
k
λ
i
∗
∇
c
i
(
x
∗
)
+
∑
i
=
1
l
μ
i
∗
∇
h
i
(
x
∗
)
=
0
这就是 KKT 条件了,第一行和第二行是原问题的约束,必须遵守;第三行则是弱对偶的必要条件。最后一行,我们知道,既然 x ∗ x^* x∗ 是最优点,那么理所当然的,原问题 L \mathcal{L} L 关于 x ∗ x^* x∗ 的导数必须等于 0。
现在难点主要在第四行,其实第四行的不等式是一个被称为“互补松弛条件”的东西。我们做一个简单的证明。
首先我们知道
f
(
x
∗
)
=
g
(
λ
∗
,
μ
∗
)
=
inf
x
L
(
x
∗
,
λ
∗
,
μ
∗
)
所以有:
f
(
x
∗
)
⩽
L
(
x
∗
,
λ
∗
,
μ
∗
)
=
f
(
x
∗
)
+
∑
i
=
1
k
λ
i
∗
c
i
(
x
∗
)
+
∑
i
=
1
l
μ
i
∗
h
i
(
x
∗
)
同时我们知道,
λ
⩾
0
\lambda \geqslant 0
λ⩾0 且
c
i
(
x
)
⩽
0
c_i(x) \leqslant 0
ci(x)⩽0,而
h
i
=
0
h_i = 0
hi=0,所以有:
f
(
x
∗
)
+
∑
i
=
1
k
λ
i
∗
c
i
(
x
∗
)
+
∑
i
=
1
l
μ
i
∗
h
i
(
x
∗
)
⩽
f
(
x
∗
)
f(x^*) + \sum_{i=1}^{k}\lambda_i^*c_i(x^*) + \sum_{i=1}^{l}\mu_i^*h_i(x^*) \leqslant f(x^*)
f(x∗)+i=1∑kλi∗ci(x∗)+i=1∑lμi∗hi(x∗)⩽f(x∗)
联立上面几个式子,有:
f
(
x
∗
)
=
g
(
λ
∗
,
μ
∗
)
=
inf
x
f
(
x
∗
)
+
∑
i
=
1
k
λ
i
∗
c
i
(
x
∗
)
+
∑
i
=
1
l
μ
i
∗
h
i
(
x
∗
)
=
f
(
x
∗
)
+
∑
i
=
1
k
λ
i
∗
c
i
(
x
∗
)
+
∑
i
=
1
l
μ
i
∗
h
i
(
x
∗
)
=
f
(
x
∗
)
注意到第二行和第三行想等,而
λ
i
c
i
⩽
0
\lambda_ic_i \leqslant 0
λici⩽0,所以为了让等式成立,必然有:
λ
i
c
i
(
x
)
=
0
\lambda_ic_i(x) = 0
λici(x)=0
这被称为互补松弛条件。
把这几个条件一股脑叠加在一起,就构成了 KKT 条件。对于目标函数和约束函数可微的优化问题,如果强对偶成立,则任意一对原问题的最优解和对偶问题的最优解满足 KKT 条件。
6.2.2 凸问题下的 KKT
当原问题为凸优化时,KKT 条件在非凸的基础上有多了找到最优点的功能
在这种情况下,那么满足 KKT 条件的点一定是原问题和对偶问题的最优解;KKT 条件成了强对偶和最优解的充要条件
也就是说:
- 若原问题是Convex的
-
∃
x
^
,
λ
^
,
μ
^
\exists \hat x, \hat \lambda, \hat \mu
∃x^,λ^,μ^ 满足:
c i ( x ^ ) ⩽ 0 i = 1 , … , k h i ( x ^ ) = 0 i = 1 , … , l λ ^ i ⩾ 0 i = 1 , … , k λ ^ i c i ( x ^ ) = 0 i = 1 , … , k ∇ f ( x ^ ) + ∑ i = 1 k λ ^ i ∇ c i ( x ^ ) + ∑ i = 1 l μ ^ i ∇ h i ( x ^ ) = 0ci(x^)⩽0hi(x^)=0λ^i⩾0λ^ici(x^)=0∇f(x^)+i=1∑kλ^i∇ci(x^)+i=1∑lμ^i∇hi(x^)=0i=1,…,ki=1,…,li=1,…,ki=1,…,k
那么 x ^ \hat x x^ 和 ( λ ^ , μ ^ ) (\hat \lambda, \hat \mu) (λ^,μ^) 分别是原问题和对偶问题的最优解,且最优对偶间隙为 0,强对偶性满足。
6.3 几种条件之间的关系的总结
-
对于任意问题
强对偶 + 最优解 ⇒ \Rightarrow ⇒ KKT条件 -
对于 Convex + 可微 的问题
KKT 条件 ⇒ \Rightarrow ⇒ 强对偶 + 最优解 -
Convex + Slater ⇒ \Rightarrow ⇒ 强对偶
7. 个人总结
本文应该是我写过的最麻烦的一篇文章了,一大堆latex公式敲起来简直酸爽。其实这篇文章的写作动机是我自己太菜了,别人的文章一大堆基础知识看不懂,什么仿射函数什么凸优化,还得自己一个一个去查,所以干脆自己写了一份阅读难度比较低(自以为)的博文。
按照原计划,本来后面应该还有几节案例分析的内容,但容我抱歉,写这个实在太累了,所以就割掉了。。
总之写作不易,转载的话随意但还请注明原链接地址,谢谢( ̄▽ ̄)"!