数学分析之拉格朗日余项与误差
拉格朗日余项与误差
拉格朗日余项
拉格朗日余项和泰勒公式密不可分。泰勒级数的全形如下: f(x)=f(a)+f′(a)(x−a)+2!f′′(a)(x−a)2+⋯+n!f(n)(a)(x−a)n+⋯=n=0∑∞n!f(n)(a)(x−a)n 其中,前n项可以称为函数在点x=a处的n阶泰勒展开式。所谓的阶,是指x的幂次;n阶就是x的最高次幂为n,而不是展开到第n项。
但是,泰勒展开能够无限地逼近原函数,是以n趋向于无穷为前提条件的。如果我们只是将函数展开到n阶,则后面的部分(我们称为余项, remainder)就被省略了,这必然会产生误差。记余项的表达式为Rn(x),用它表示n项之后的余项(注意下标是 n 而不是 n+1),我们可以将泰勒展开写成如下形式: f(x)=f(a)+f′(a)(x−a)+2!f′′(a)(x−a)2+⋯+n!f(n)(a)(x−a)n+Rn(x) 或者说 f(x)=Pn(x)+Rn(x) 这式子的意思是原函数可以分解为两个部分,一部分是 n 阶泰勒展开,另一部分就是拉格朗日余项。那么,做一个移项,就可以有:Rn(x)=f(x)−Pn(x)。
这就是说,用n阶幂级数来逼近原函数,其误差就是这一余项。而拉格朗日余项就是表达这些被省略部分的一个公式,我们可以用它来估计误差。为此,我们先写出函数的第 n+1 阶展开式: (n+1)!f(n+1)(a)(x−a)n+1 而拉格朗日余项(在具体题目中,我们也称为拉格朗日误差界 Lagrange Error Bound) 在形式上就类似于函数的第 n+1 阶,其表达式如下: Rn(x)=(n+1)!f(n+1)(c)(x−a)n+1,c在x与a之间。 需要注意的是,c只是在x与a之间,可能是x≤c≤a,也可能是a≤c≤x。同时,拉格朗日余项定理像微分中值定理(Mean Value Theorem)、介值定理(Intermediate Value Theorem)一样,都是存在性定理,即只能告知值的存在(我们知道有这样一个值),但不能告知其具体位置(但不知道它到底是多少)。如果我们使用麦克劳林式(Maclaurin Series,即a=0时的特殊形式),就可以将拉格朗日余项变成较简单的形式: Rn(x)=(n+1)!f(n+1)(c)xn+1,c在x与0之间。
拉格朗日误差界
观察拉格朗日余项定理的形式,对于给定a、n和x的情况下,如果要确定这个余项的界限,唯一要确定的就是前面的这个第 n+1 阶导数的取值范围。若令有正数M=∣f(n+1)(c)∣,则只需要确定M的范围,那么,整个余项的范围也就唯一给定了。由于误差值可能为正,也可能为负,为便利讨论,我们一般都取其绝对值进行考查,即 ∣Rn(x)∣=∣(n+1)!f(n+1)(c)(x−a)n+1∣=(n+1)!M∣(x−a)n+1∣ 而对于麦克劳林式,我们就变成考查: ∣Rn(x)∣=∣(n+1)!f(n+1)(c)xn+1∣=(n+1)!M∣xn+1∣ 这时我们就要介绍一个基本定理,即拉格朗日余项定理:
若存在正数Max,使得对任意ξ,如果a≤ξ≤x或x≤ξ≤a,均有∣f(n+1)(ξ)∣≤M,则: ∣Rn(x)∣=∣(n+1)!f(n+1)(c)(x−a)n+1∣≤(n+1)!M∣(x−a)n+1∣ 也就是说M的取值范围其实就由∣f(n+1)(ξ)∣,(a≤ξ≤x或x≤ξ≤a)唯一给定。这一不等式也叫泰勒不等式。这是我们进行余项范围估计的主要理论基础。
例题
例1 将y=sin(x)展开成麦克劳林式,并估计其误差:
根据基本公式:sin(x)=x−3!1x3+5!1x5−7!1x7+⋯+(−1)n(2n+1)!x2n+1+⋯,很容易得出5阶麦克劳林式:sin(x)≈x−3!1x3+5!1x5
其余项按照拉格朗日余项定理,可以写成(注意:5阶的余项是6次方): R5(x)=6!f6(c)x6,c在0和x之间 而∣f6(x)∣=∣−sin(x)∣≤1,所以R5(x)≤6!x6。
例2 将y=sin(x)展开成麦克劳林式,据此估计sin 0.2的值,并计算其误差。
使用例1结论:sin(0.2)≈0.2−3!1(0.2)3+5!1(0.2)5≈0.1986693333
同时,R5(0.2)≤6!0.26=8.888889∗10−8
交错级数
在一些情况下,使用交错级数计算误差相对简单,其基本定理如下:
若交错级数n=0∑∞un=n=0∑∞(−1)n+1(vn)满足以下条件:
- 正项递减,即0≤vn+1≤vn;
- 正项趋零,即x→+∞limvn=0
则必有其余项的范围∣Rn(x)∣=∣S−Sn∣<∣un+1∣=vn+1
其中,S表示全部和,Sn表示部分和,也就是我们高中数学里习惯说的前n项和。简单的讲,交错级数前n项和的余项,不会超过接下来这一项的绝对值,这就是交错级数的余项公式。
拉格朗日插值余项
在插值过程中,有一个拓展概念叫拉格朗日插值余项。取插值结点:a≤x0<x1<⋅⋅⋅⋅⋅⋅<xn≤b 满足Ln(xk)=f(xk)的 n 次多项式插值余项: Rn(x)=f(x)−Ln(x)=(n+1)!f(n+1)(ξn)ωn+1(x) 其中,ωn+1(x)=(x−x0)(x−x1)⋯(x−xn)。选取:x0,x1,⋯,xn,使a≤x≤bmax∣ωn+1(x)∣=min
结论:选取切比雪夫多项式Tn+1(x)的全部零点。
使用切比雪夫节点插值和等距插值对函数f(x)=1+x21模拟:
Figure 1: 切比雪夫结点插值
插值函数L10(x)取切比雪夫结点插值
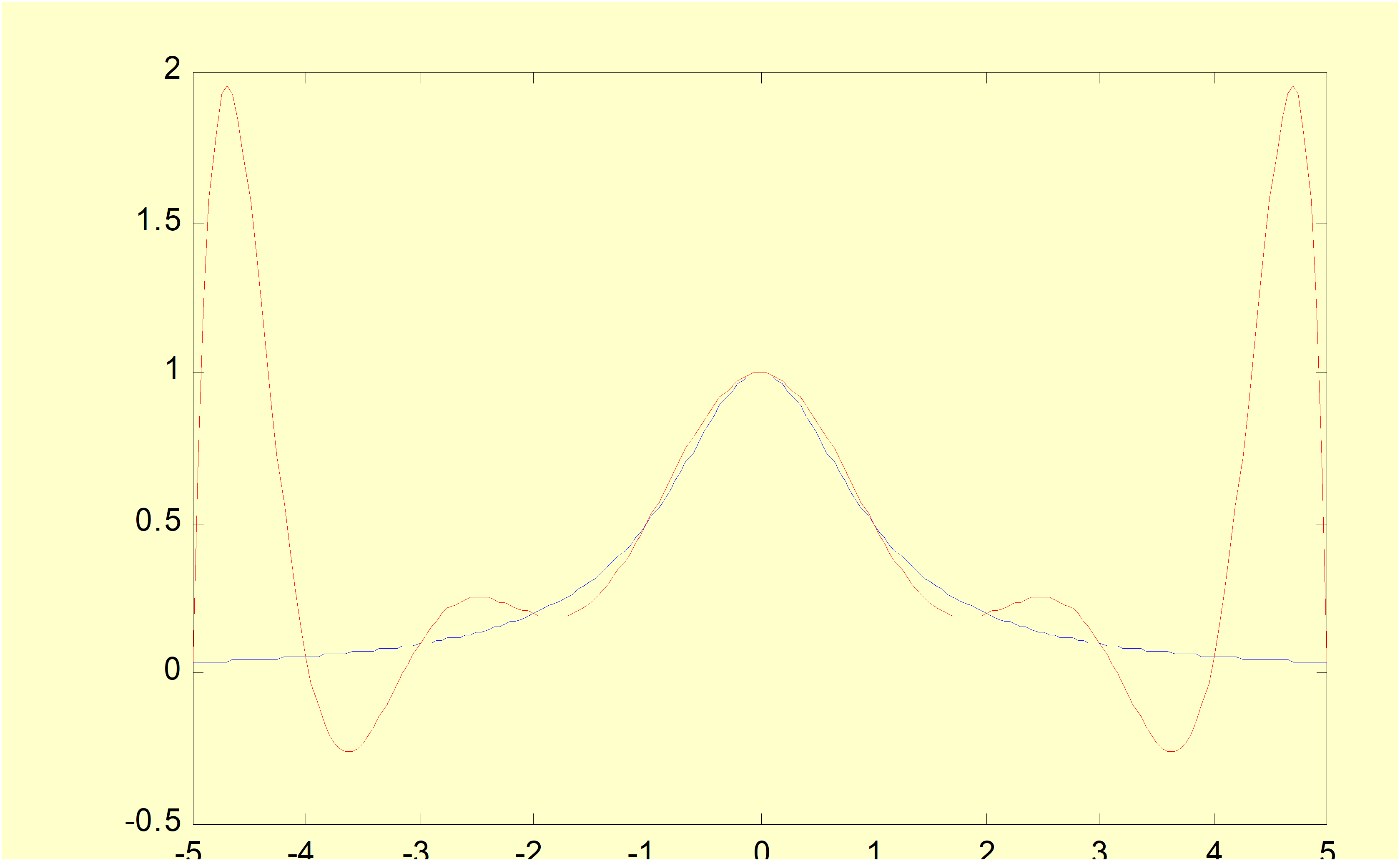
Figure 2: 等距结点插值
插值函数L10(x)取等距结点插值

